
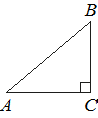
 В треугольнике ABC угол C равен 90°, AB=25, AC=24. Найдите cosB.
В треугольнике ABC угол C равен 90°, AB=25, AC=24. Найдите cosB.
По определению:
cosB=BC/AB
Чтобы найти BC можно использовать
теорему Пифагора:
AB2=BC2+AC2
252=BC2+242
625=BC2+576
BC2=49
BC=7
Теперь можем найти косинус:
cosB=BC/AB=7/25=0,28
Ответ: 0,28
Поделитесь решением
Присоединяйтесь к нам...
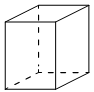 Два ребра прямоугольного параллелепипеда равны 8 и 5,
а объём параллелепипеда равен 280. Найдите площадь поверхности этого параллелепипеда.
Два ребра прямоугольного параллелепипеда равны 8 и 5,
а объём параллелепипеда равен 280. Найдите площадь поверхности этого параллелепипеда.
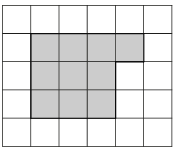 План местности разбит на клетки. Каждая клетка обозначает квадрат 1м х 1м. Найдите площадь участка, выделенного на плане. Ответ дайте
в квадратных метрах.
План местности разбит на клетки. Каждая клетка обозначает квадрат 1м х 1м. Найдите площадь участка, выделенного на плане. Ответ дайте
в квадратных метрах.
 В треугольнике ABC угол C равен 90°, AB=25, AC=24. Найдите cosB.
В треугольнике ABC угол C равен 90°, AB=25, AC=24. Найдите cosB.
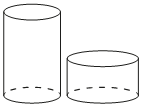 Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 9, а второго — 9 и 2.
Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 9, а второго — 9 и 2.
Во сколько раз объём первого цилиндра больше объёма второго?
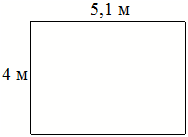 На плане указано, что прямоугольная комната имеет площадь 20,1 кв. м. Точные измерения показали, что ширина комнаты равна 4 м,
а длина 5,1 м. На сколько квадратных метров площадь комнаты отличается от площади, указанной на плане?
На плане указано, что прямоугольная комната имеет площадь 20,1 кв. м. Точные измерения показали, что ширина комнаты равна 4 м,
а длина 5,1 м. На сколько квадратных метров площадь комнаты отличается от площади, указанной на плане?





Комментарии: