Задача №7 из 18 |
В ящике находятся чёрные и белые шары, причём чёрных в 4 раза больше, чем белых. Из ящика случайным образом достали один шар. Найдите вероятность того, что он будет белым.
Пусть х - количество белых шаров, тогда 4х - количество черных.
Всего шаров х+4х=5х
Вероятность любого события равна отношению числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.
В данной задаче интересующее нас событие - выбор белого шара.
Т.е. выбор одного из х шаров - благоприятный исход
Полная группа исходов (благоприятных и неблагоприятных) = 5х.
P=х/(5х)=1/5=0,2
Ответ: 0,2
Поделитесь решением
Присоединяйтесь к нам...
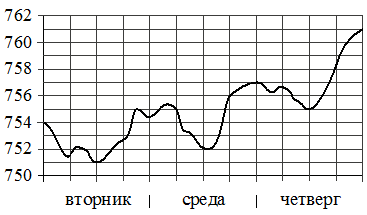На рисунке изображён график значений атмосферного давления в некотором городе за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба.
Определите по рисунку наименьшее значение атмосферного давления
за данные три дня (в миллиметрах ртутного столба).
Вероятность того, что стекло мобильного телефона разобьётся при падении на твёрдую поверхность, равна 0,84. Найдите вероятность того, что при падении на твёрдую поверхность стекло мобильного телефона не разобьётся.
В среднем из 1400 садовых насосов, поступивших в продажу, 14 подтекает. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
В среднем из 500 садовых насосов, поступивших в продажу, 25 подтекает. Найдите вероятность того, что случайно выбранный для контроля насос подтекает.
В фирме такси в наличии 20 легковых автомобилей: 7 из них чёрного цвета с жёлтыми надписями на боках, остальные — жёлтого цвета с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: