
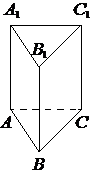
 Сторона основания правильной треугольной призмы ABCA1B1C1 равна 2, а высота этой призмы равна 4√3. Найдите объём призмы ABCA1B1C1.
Сторона основания правильной треугольной призмы ABCA1B1C1 равна 2, а высота этой призмы равна 4√3. Найдите объём призмы ABCA1B1C1.
Объем призмы вычисляется перемножением площади основания призмы на высоту.
Найдем площадь основания.
По
определению правильной призмы, в основании лежит правильный (т.е.
равносторонний) треугольник.
По
пятому свойству равностороннего треугольника:
S=a2√3/4=22√3/4=4√3/4=√3
Зная площадь основания и высоту, вычисляем объем призмы:
V=S*h=√3*4√3=4(√3)2=4*3=12
Ответ: 12
Поделитесь решением
Присоединяйтесь к нам...
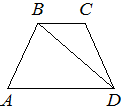 В трапеции ABCD известно, что AB=CD, ∠BDA=54° и ∠BDC=23°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции ABCD известно, что AB=CD, ∠BDA=54° и ∠BDC=23°. Найдите угол ABD. Ответ дайте в градусах.
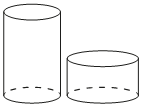 Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 9, а второго — 9 и 2.
Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 9, а второго — 9 и 2.
Во сколько раз объём первого цилиндра больше объёма второго?
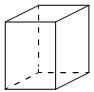 Два ребра прямоугольного параллелепипеда равны 8 и 2, а объём параллелепипеда равен 144. Найдите площадь поверхности этого параллелепипеда.
Два ребра прямоугольного параллелепипеда равны 8 и 2, а объём параллелепипеда равен 144. Найдите площадь поверхности этого параллелепипеда.
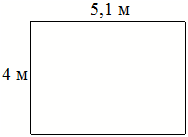 На плане указано, что прямоугольная комната имеет площадь 20,1 кв. м. Точные измерения показали, что ширина комнаты равна 4 м,
а длина 5,1 м. На сколько квадратных метров площадь комнаты отличается от площади, указанной на плане?
На плане указано, что прямоугольная комната имеет площадь 20,1 кв. м. Точные измерения показали, что ширина комнаты равна 4 м,
а длина 5,1 м. На сколько квадратных метров площадь комнаты отличается от площади, указанной на плане?
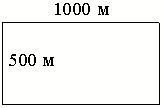 Участок земли под строительство санатория имеет форму прямоугольника, стороны которого равны 1000 м и 500 м. Одна из больших сторон участка идёт вдоль моря, а три остальные стороны нужно оградить забором. Найдите длину этого забора. Ответ дайте
в метрах.
Участок земли под строительство санатория имеет форму прямоугольника, стороны которого равны 1000 м и 500 м. Одна из больших сторон участка идёт вдоль моря, а три остальные стороны нужно оградить забором. Найдите длину этого забора. Ответ дайте
в метрах.
Комментарии: