
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и значениями их производной в точке x=1.
ГРАФИКИ
А) 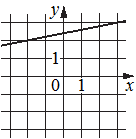 Б)
Б) 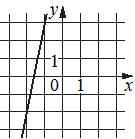 В)
В) 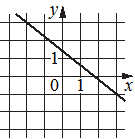 Г)
Г) 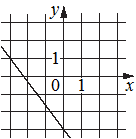
ЗНАЧЕНИЯ ПРОИЗВОДНОЙ
1) 0,2
2) -4/3
3) -0,8
4) 5
В таблице под каждой буквой укажите соответствующий номер.
Про условию данной задачи сразу надо дать комментарий.
Производная от линейной функции (чем и является y=kx+b) - величина постоянная, т.е. при любом значении х производная меняться не будет, поэтому фраза "значениями их производной в точке x=1" смысла не имеет.
Скорее всего, это единое условие для целой группы задач, где будут присутствовать не только линейные функции, тогда это фраза обязательна.
Приступим к решению.
y'=(kx+b)'=k
Т.е. производная от этой функции - это коэффициент k.
Чтобы его найти, надо посмотреть на график и подставить в уравнение прямой две точки графика (т.е. значения x и y) и решить полученную систему уравнений.
Рассмотрим график А).
Лучше выбирать точку с целыми значениями x и y, тогда вычисления будут точными.
По графику А) видим, что ему принадлежат точки (-2;2) и (3;3).
Подставляем их в функцию:
Для первой точки: 2=-2k+b
Для второй точки: 3=3k+b
Это и есть система уравнений, которую надо решить любым способом и найти k - это и будет производная для первой функции.
Легче всего будет вычесть из второго уравнения первое, чтобы избавиться от b (это один из способов решения системы уранений):
3-2=3k+b-(-2k+b)
1=3k+b+2k-b
1=5k
k=1/5=0,2
Т.е. для графика А) ответ 1).
Рассмотрим график Б):
(-2;-2) и (-1;3) - точки, принадлежащие графику.
-2=-2k+b
3=-k+b
Полученная система уравнений, точно также вычтем из второго первое:
3-(-2)=-k+b-(-2k+b)
3+2=-k+b+2k-b
5=k - ответ 4)
График В).
(-2;3) и (3;-1) - точки.
3=-2k+b
-1=3k+b
Вычитаем:
-1-3=3k+b-(-2k+b)
-4=3k+b+2k-b
-4=5k
k=-4/5=-0,8 - ответ 3)
График Г).
(-3;1) и (0;-3) - точки.
1=-3k+b
-3=0*k+b => -3=b
Сейчас можно не вычитать, а просто подставить полученное значение b в первое уравнение:
1=-3k-3
3k=-3-1
3k=-4
k=-4/3 - ответ 2).
Ответ:
| График | А) | Б) | В) | Г) |
| Производная | 1) | 4) | 3) | 2) |
Поделитесь решением
Присоединяйтесь к нам...
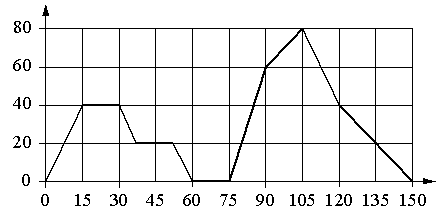 На рисунке точками показаны объёмы месячных продаж холодильников
в магазине бытовой техники. По горизонтали указываются месяцы,
по вертикали — количество проданных холодильников. Для наглядности точки соединены линией.
На рисунке точками показаны объёмы месячных продаж холодильников
в магазине бытовой техники. По горизонтали указываются месяцы,
по вертикали — количество проданных холодильников. Для наглядности точки соединены линией.
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику продаж холодильников.
| ИНТЕРВАЛЫ ВРЕМЕНИ | ХАРАКТЕРИСТИКИ |
| А) январь-март | 1) продажи за первый и второй месяцы квартала совпадают |
| Б) апрель-июнь | 2) ежемесячный объём продаж достигает максимума за весь период |
| В) июль-сентябрь | 3) за этот период ежемесячный объём продаж увеличился на 300 холодильников |
| Г) октябрь-декабрь | 4) за последний месяц периода было продано меньше 200 холодильников |
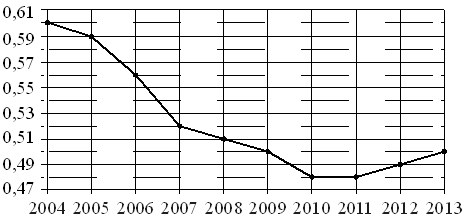 На рисунке точками показан прирост населения Китая в период с 2004 по 2013 годы. По горизонтали указывается год, по вертикали — прирост населения в процентах (увеличение численности населения относительно прошлого года). Для наглядности точки соединены линией.
На рисунке точками показан прирост населения Китая в период с 2004 по 2013 годы. По горизонтали указывается год, по вертикали — прирост населения в процентах (увеличение численности населения относительно прошлого года). Для наглядности точки соединены линией.
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику прироста населения Китая.
| ПЕРИОДЫ ВРЕМЕНИ | ХАРАКТЕРИСТИКИ |
| А) 2005–2007 гг. | 1) падение прироста остановилось |
| Б) 2007–2009 гг. | 2) наибольшее падение прироста населения |
| В) 2009–2011 гг. | 3) прирост населения находился в пределах от 0,5% до 0,52% |
| Г) 2011–2013 гг. | 4) прирост населения увеличивался |
На рисунках изображены графики функций вида y=ax2+bx+c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
ФУНКЦИИ
А) 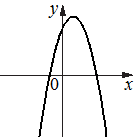 Б)
Б) 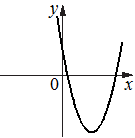 В)
В) 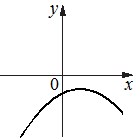 Г)
Г) 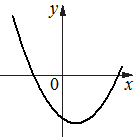
КОЭФФИЦИЕНТЫ
1) a<0, c<0
2) a<0, c>0
3) a>0, c>0
4) a>0, c<0
В таблице под каждой буквой укажите соответствующий номер.
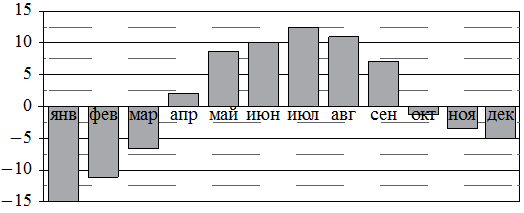 На диаграмме показана среднемесячная температура воздуха
в Петрозаводске за каждый месяц 1976 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия.
На диаграмме показана среднемесячная температура воздуха
в Петрозаводске за каждый месяц 1976 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия.
Определите по диаграмме наименьшую среднемесячную температуру
во второй половине 1976 года. Ответ дайте в градусах Цельсия.
Установите соответствие между графиками функций и характеристиками этих функций на отрезке [-1;1].
ГРАФИКИ
А) 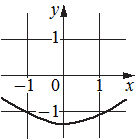 Б)
Б) 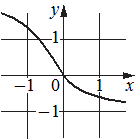 В)
В) 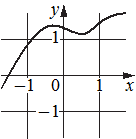 Г)
Г) 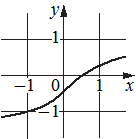
ХАРАКТЕРИСТИКИ
1) функция принимает отрицательное значение в каждой точке отрезка [-1;1]
2) функция возрастает на отрезке [-1;1]
3) функция принимает положительное значение в каждой точке отрезка [-1;1]
4) функция убывает на отрезке [-1;1]
В таблице под каждой буквой укажите соответствующий номер.
Комментарии: