
Постройте график функции 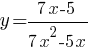 и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Определим Область Допустимых Значений (ОДЗ):
Так как делить на 0 нельзя, то 7x2-5x≠0
Найдем такие х:
x(7x-5)≠0
Произведение равно нулю, когда один из множителей равен нулю, поэтому рассмотрим два варианта:
1) x1≠0
2) 7x-5≠0
x2≠5/7
Таким образом, мы получили значения, которые НЕ МОЖЕТ принимать х.
Теперь можем упростить:
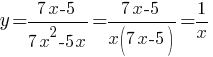
 График данной функции представляет из себя обычную гиперболу с исключенной точкой при х=5/7 (из ОДЗ).
График данной функции представляет из себя обычную гиперболу с исключенной точкой при х=5/7 (из ОДЗ).
Построим график по точкам:
| X | 0,5 | 1 | 2 | -0,5 | -1 | -2 |
| Y | 2 | 1 | 0,5 | -2 | -1 | -0,5 |
 y=1/x
y=1/x Заметим, что в нашем графике есть "выколотая" точка при x=5/7, через которую может пройти искомая прямая.
Заметим, что в нашем графике есть "выколотая" точка при x=5/7, через которую может пройти искомая прямая.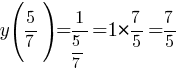
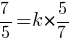
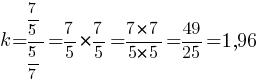
Поделитесь решением
Присоединяйтесь к нам...
 Две прямые пересекаются в точке C (см. рис.). Найдите абсциссу точки C.
Две прямые пересекаются в точке C (см. рис.). Найдите абсциссу точки C.
Постройте график функции
 -x2, если |x|≤1
-x2, если |x|≤1
1/x, если |x|>1
и определите, при каких значениях c прямая y=c будет иметь с графиком единственную общую точку.
 На рисунке изображены графики функций y=6-x2 и y=5x. Вычислите абсциссу точки B.
На рисунке изображены графики функций y=6-x2 и y=5x. Вычислите абсциссу точки B.
Известно, что графики функций y=x2+p и y=-2x-2 имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
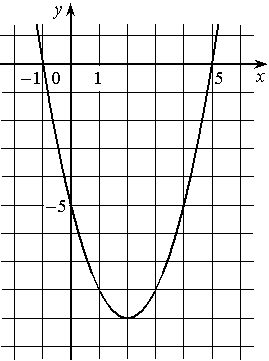 На рисунке изображён график квадратичной функции y=f(x).
На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции являются верными? Запишите их номера.
1) f(-1)=f(5)
2) Функция убывает на промежутке [2; +∞)
3) f(x)>0 при x<-1 и при x>5
Комментарии:
(2021-11-26 13:45:51) Александра: общая точка с прямой y = 11 x- 76.
(2020-11-25 11:59:06) Юлия: Через точку О пересечения диагоналей параллелограмма ABCD проведена прямая пересекающая стороны BC и AD в точках к и м соответственно Докажите что отрезки ВК и DМ равны
(2018-01-15 12:27:44) Администратор: Джон Титор, я немного расписал решение, надеюсь стало понятней. Если нет - пишите.
(2017-12-19 17:04:17) Джон Титор: А почему вторая точка 7/5? Я немного туплю
(2017-05-12 23:36:53) Администратор: Виолета, эта точка взята из ОДЗ. Я подкорректировал решение, надеюсь, теперь стало понятней. P.S. А разве Ваше имя пишется не с двумя \"т\"? Виолетта...
(2017-05-11 17:41:36) Виолета: \"График данной функции представляет из себя обычную гиперболу с исключенной точкой при х=5/7.\" Как была определена данная точка?
(2016-12-20 23:21:20) Администратор: Ира, потому что прямая y=kx при любом k проходит через точку (0;0). Это легко понять, если подставить эти координаты в уравнение: 0=k0 - верное равенство.
(2016-12-20 22:53:39) ира: Почему вторая точка прямой (0,0), а не какая-нибудь другая?
(2015-05-14 21:42:09) Администратор: Виктория, Вы, наверно, имеете в виду строку D=-4k*(-1)=4k, так это дискриминант, вычисляемый строго по формуле D=b2-4ac.
(2015-05-14 19:42:26) Виктория: Откуда взялась 4 в квадратном уравнении?
(2015-05-11 20:36:06) Администратор: Акулина, мы чертили только график функции 1/x, про какие степени Вы говорите? Перефразируйте, пожалуйста, свой вопрос.
(2015-05-11 18:59:57) Акулина: а почему мы чертили гиперболу в первой и второй степенях?
(2015-04-09 13:11:02) Администратор: Я добавил в решение точки, по которым можно построить гиперболу.
(2015-04-09 12:35:57) Администратор: Ксения, не две, это одна гипербола. Функция может иметь разрыв графика, это ничему не противоречит.
(2015-04-09 11:58:04) ксения: что-то ничего не понятно, почему здесь две гиперболы? ведь функция одна и без модуля(
(2015-04-09 11:50:21) : а вы сможете подсказать, какие лучше значения брать в таблице для гиперболы ?
(2015-04-08 16:28:19) Администратор: 1,4=k5/7 домножили на 7, получилось 1,4*7=(k5/7)*7 => 9,8=5k
(2015-04-08 16:26:14) Администратор: В данном случае k - это коэффициент "а" в квадратном уравнении, а по определению квадратного уравнения "а" не равен нулю.
(2015-04-08 15:26:57) : и как вы получили 9,8?
(2015-04-08 15:23:36) : а что именно нарушается в определении?