
Установите соответствие между графиками функций и формулами, которые их задают. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
| ФОРМУЛЫ | Графики | ||
|
1) y=-x2+7x-14 2) y=x2-7x+14 3) y=x2+7x+14 4) y=-x2-7x-14 |
A)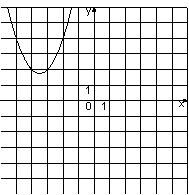
|
Б)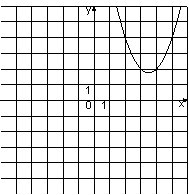
|
В)
|
Все формулы представляют из себя
квадратичные функции.
В функциях 2) и 3) а - положительный, значит, ветви параболы направлены вверх.
В функциях 1) и 4) а - отрицательный, значит, ветви параболы направлены вниз.
Найдем координаты вершин парабол, чтобы определить какой график какой функции соответствует.
Координату x0 можно найти по формуле: x0=-b/2a
1) x0=-7/(2(-1))=3,5
2) x0=-(-7)/(2*1)=3,5
3) x0=-7/(2*1)=-3,5
4) x0=-(-7)/(2*(-1))=-3,5
Итак, резюмируем:
1) Ветви вниз, x0=3,5
Никакой график не подходит
2) Ветви вверх, x0=3,5
Подходит только график Б)
3) Ветви вверх, x0=-3,5
Подходит только график A)
4) Ветви вниз, x0=-3,5
Подходит только график B)
Ответ: А) - 3), Б) - 2), В) - 4)
Поделитесь решением
Присоединяйтесь к нам...
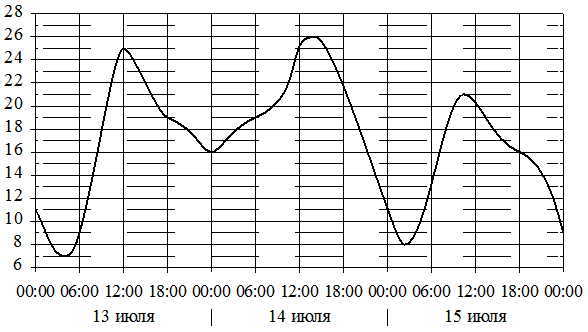 На графике показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по графику наименьшую температуру воздуха 13 июля. Ответ дайте в градусах Цельсия.
На графике показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по графику наименьшую температуру воздуха 13 июля. Ответ дайте в градусах Цельсия.
Постройте график функции 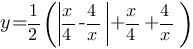 и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Постройте график функции
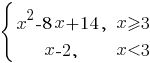
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Постройте график функции
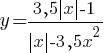
Определите, при каких значениях k прямая y=kx не имеет с графиком общих точек.
Постройте график функции y=x2-6|x|+8. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
Комментарии:
(2017-01-14 01:10:24) Администратор: Кирилл, даже не знаю, как вкралась эта опечатка. Спасибо большое, что заметили. Все исправлено.
(2017-01-14 00:13:35) Кирилл: вы же писали "В функциях 1) и 3) а - положительный, значит, ветви параболы направлены вверх", но когда резюмируем, у 1) уже ветви вниз, как так?