Постройте график функции
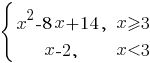
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Чтобы построить график этой функции, надо построить график каждой подфункции на указанных для подфункций диапазонах.
y1=x2-8x+14 на диапазоне [3;+∞)
y2=x-2 на диапазоне (-∞;3)
Построим графики по точкам (красный график):
| X | 3 | 4 | 5 | 6 |
| Y | -1 | -2 | -1 | 2 |
| X | 3 | 2 | 1 |
| Y | -1 | 0 | -1 |
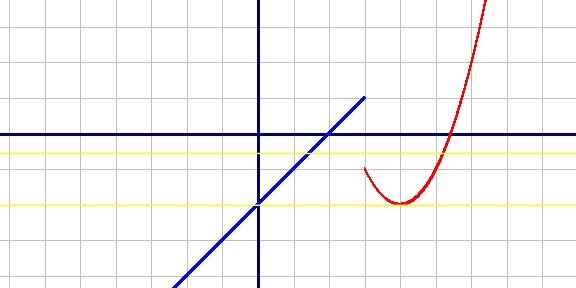y=m - это прямые, параллельные оси Х. Желтым цветом построены прямые y=m. Прямая y=m будет иметь ровно две общие точки с графиком, когда эта прямая касается вершины параболы и на диапазоне по оси Y от -1 до 1.Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции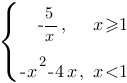 
и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
Постройте график функции y=|x|(x+1)-6x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Постройте график функции
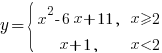
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Постройте график функции
x2-4x+4 при x≥-1
-9/x при x<-1
и определите, при каких значениях m прямая y=m имеет с графиком одну или две общие точки.
Постройте график функции
-x2, если |x|≤1
1/x, если |x|>1
и определите, при каких значениях c прямая y=c будет иметь с графиком единственную общую точку.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: