
Постройте график функции
 -x2, если |x|≤1
-x2, если |x|≤1
1/x, если |x|>1
и определите, при каких значениях c прямая y=c будет иметь с графиком единственную общую точку.
Чтобы построить график функции состоящей из двух подфункций, необходимо построить график каждой подфункции на указанных для них диапазонах и объединить эти графики.
Так как в данном примере диапазоны обозначены неравенствами с
функцией модуля, то сначала решим эти неравенства:
Функция |x| всегда принимает положительные значения, и |x| будет меньше или равен 1, когда -1≤х≤1, т.е. x⊂[-1;1].
Следовательно |x|>1 на всем остальном пространстве, т.е. x⊂(-∞;-1)∪(1;+∞).
Запишем получившуюся функцию:
 -x2, если x⊂[-1;1]
-x2, если x⊂[-1;1]
1/x, если x⊂(-∞;-1)∪(1;+∞)
Построим по точкам график обоих подфункций в указанных диапазонах:
-x2, если x⊂[-1;1]
| X | -1 | 0 | 1 |
| Y | -1 | 0 | -1 |
| X | -5 | -2 | -1 | 1 | 2 | 5 |
| Y | -0,2 | -0,5 | -1 | 1 | 0,5 | 0,2 |
 График первой подфункции начерчен красным цветом, график второй подфункции - синим.
График первой подфункции начерчен красным цветом, график второй подфункции - синим.Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции y=x2-6|x|+2x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
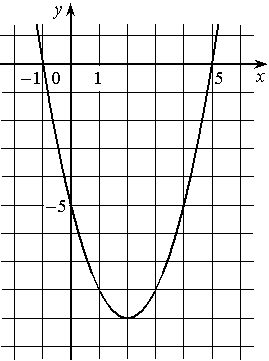 На рисунке изображён график квадратичной функции y=f(x).
На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции являются верными? Запишите их номера.
1) f(-1)=f(5)
2) Функция убывает на промежутке [2; +∞)
3) f(x)>0 при x<-1 и при x>5
Постройте график функции
 -x2+10x-21 при x≥3
-x2+10x-21 при x≥3
-x+3 при x<3
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Установите соответствие между функциями и их графиками.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | |||
|
А) y=3x Б) y=-3x В) y=(1/3)x |
1) 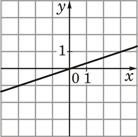 |
2) 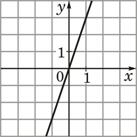 |
3) 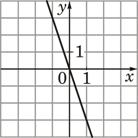 |
4)  |
 На рисунке изображён график квадратичной функции y=f(x).
На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции являются верными? Запишите их номера.
1) f(-1)=f(5)
2) Функция убывает на промежутке [2; +∞)
3) f(x)>0 при x<-1 и при x>5
Комментарии:
(2022-04-07 08:51:40) Александра: Задание 4.1.153 из сборника вариантов Огэ 2022
(2015-05-10 18:43:56) Татьяна: Огромное спасибо! Я впервые столкнулась с таким заданием, а Вы так здорово все объяснили!!!! Еще раз спасибо!!1