
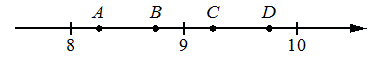 На координатной прямой отмечены точки A, B, C, D. Одна из них соответствует числу √
На координатной прямой отмечены точки A, B, C, D. Одна из них соответствует числу √
1) точка A
2) точка B
3) точка C
4) точка D
Чтобы решить эту задачу, надо обозначенные числа 8, 9 и 10 привести к такому же виду, как сравниваемое число, т.е. к виду "что-то" под корнем.
Для этого возведем числа 8, 9 и 10 в квадрат, а результат запишем под корнем:
8=√
9=√
10=√
Очевидно, что √
Или 9<√
Следовательно, √
Так же очевидно, что √
Ответ: 4)
Поделитесь решением
Присоединяйтесь к нам...
Решите систему неравенств 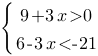
На каком рисунке изображено множество её решений?
1) 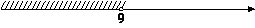
2) 
3) 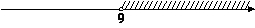
4) 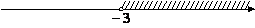
Постройте график функции 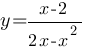 и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
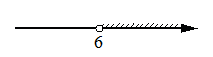
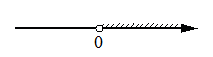
Укажите решение неравенства
6x-x2<0.
1) 
2) 
3) 
4) 
На рисунке изображены графики функций вида y=kx+b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
КОЭФФИЦИЕНТЫ
А) k<0, b>0
Б) k>0, b<0
В) k<0, b<0
1) 2)
2) 3)
3)
Какому из следующих чисел соответствует точка, отмеченная на координатной прямой?

1) 10/23
2) 12/23
3) 13/23
4) 14/23
Комментарии: