
Постройте график функции 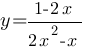 и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Запишем Область Допустимых Значений (ОДЗ).
Так как на ноль делить нельзя, то 2x2-x≠0
x(2x-1)≠0
1) x1≠0
2) 2x-1≠0 => x2≠1/2
Упростим выражение:

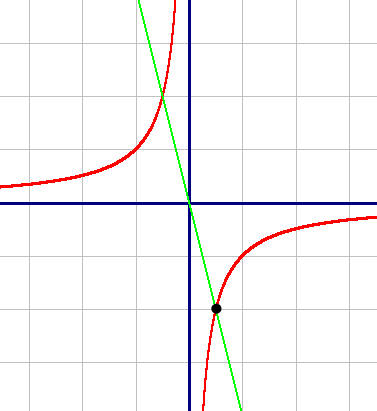
График будет гиперболой, построим его по точкам:
| X | 0,5 | 1 | 2 | -0,5 | -1 | -2 |
| Y | -2 | -1 | 0,5 | 2 | 1 | 0,5 |
Поделитесь решением
Присоединяйтесь к нам...
На рисунке изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ
А)  Б)
Б)  В)
В) 
КОЭФФИЦИЕНТЫ
1) k<0, b<0
2) k>0, b<0
3) k>0, b>0
На каком рисунке изображено множество решений системы неравенств
 x>-1,
x>-1,
-4-x>0?
1) 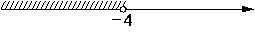
2) 
3) 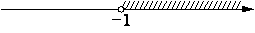
4) система не имеет решений
На координатной прямой отмечены числа a и b.
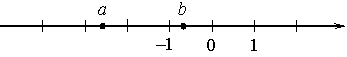
Какое из следующих утверждений неверно?
1) a+b<0
2) -2<b-1<-1
3) a2b<0
4) -a<0
Известно, что число m отрицательное. На каком из рисунков точки с координатами 0, m, 2m, m2 расположены на координатной прямой в правильном порядке?
1) 
2) 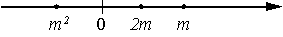
3) 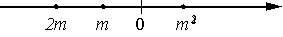
4) 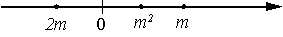
На каком рисунке изображено множество решений системы неравенств
 x>3,
x>3,
4-x<0?
1) 
2) 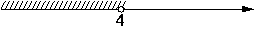
3) 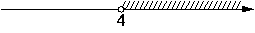
4) 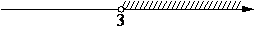
Комментарии: