На координатной прямой отмечены числа a и b.
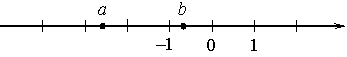
Какое из следующих утверждений неверно?
1) a+b<0
2) -2<b-1<-1
3) a2b<0
4) -a<0
Рассмотрим числа а и b.
а - отрицательное число, причем -3<a<-2
b - тоже отрицательное число, причем -1<b<0
Рассмотрим каждое утверждение:
1) a+b<0
Сложим почленно выписанные неравенства:
-3+(-1)<a+b<-2+0
-4<a+b<-2
Т.е. a+b всегда будет меньше -2, следовательно и меньше 0 - данное утверждение верно.
2) -2<b-1<-1
Вычтем из неравенства -1<b<0 почленно единицу:
-1-1<b-1<0-1
-2<b-1<-1
Т.е. данное утверждение верно
3) a2b<0
Здесь пойдем логическим путем:
a2 - это всегда положительное число (так как квадрат любого числа положителен).
a2b - отрицательное число, так как b - отциательное по условию. А "плюс на минус дают минус", т.е. меньше нуля, следовательно данное утверждение верно.
4) -a<0
Мы знаем, что -3<a<-2, домножим все числа на -1 (при этом не забудем, что знак неравенства меняется на противоположный):
-3*(-1)>a*(-1)>-2*(-1)
3>-a>2
Нас интересует только вторая часть неравенства: -a>2, т.е. данное утверждение неверно
Ответ: 4)
Поделитесь решением
Присоединяйтесь к нам...
На координатной прямой отмечены числа a и x.
Какое из следующих чисел наименьшее?
1) a+x
2) x/2
3) -a
4) a-x
На рисунке изображены графики функций вида y=kx+b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
КОЭФФИЦИЕНТЫ
А) k<0, b>0
Б) k>0, b<0
В) k<0, b<0
1)
2)
3)
Одна из точек, отмеченных на координатной прямой, соответствует числу 4/5. Какая это точка?
1) A
2) B
3) C
4) D
На каком из рисунков изображено решение неравенства 81x2<16?
1) 
2) 
3) 
4) 
На каком из рисунков изображено решение неравенства 6x-x2>0?
1) 
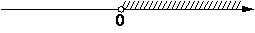
2) 
3) 
4) 
Хочу получать новые решения
Ни какого спама
Автор: Таська
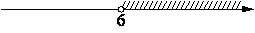
Комментарии:
(2023-12-24 16:27:57) : срочно сколько лет цою?!?!
(2023-12-24 16:27:39) : срочно сколько лет цою?!?!