
Постройте график функции 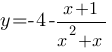 и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
Запишем Область Допустимых Значений (ОДЗ).
Так как на ноль делить нельзя, то x2+x≠0
x(x+1)≠0
x1≠0
x2≠-1
Упростим выражение:
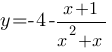
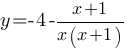
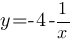
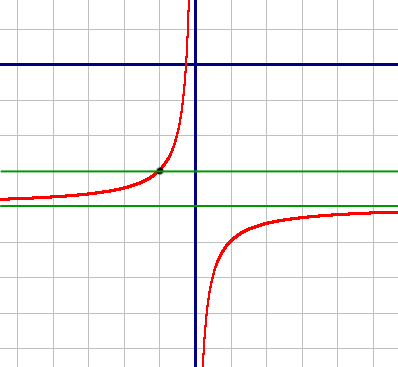 График будет гиперболой, построим его по точкам:
График будет гиперболой, построим его по точкам:
| X | -1 | -0,25 | 1 | 2 |
| Y | -3 | 0 | -5 | -4,5 |
Поделитесь решением
Присоединяйтесь к нам...
На рисунке изображены графики функций вида y=kx+b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | ||
|
А) k<0, b<0 Б) k<0, b>0 В) k>0, b<0 |
1)  |
2)  |
|
3)  |
4)  |
Постройте график функции
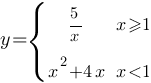 и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
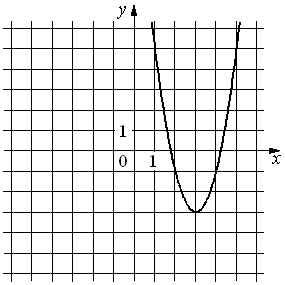 На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
| УТВЕРЖДЕНИЯ | ПРОМЕЖУТКИ |
| А) Функция возрастает на промежутке Б) Функция убывает на промежутке |
1) [0; 2] 2) [2; 5] 3) [4; 7] 4) [1; 7] |
Найдите все значения k, при каждом из которых прямая y=kx имеет с графиком функции y=x2+6,25 ровно одну общую точку. Постройте этот график и все такие прямые.
 Две прямые пересекаются в точке C (см. рис.). Найдите абсциссу точки C.
Две прямые пересекаются в точке C (см. рис.). Найдите абсциссу точки C.
Комментарии: