
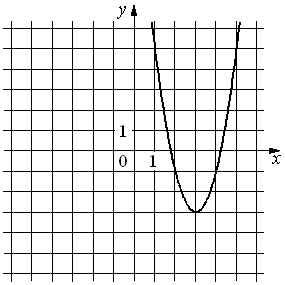
 На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
| УТВЕРЖДЕНИЯ | ПРОМЕЖУТКИ |
| А) Функция возрастает на промежутке Б) Функция убывает на промежутке |
1) [0; 2] 2) [2; 5] 3) [4; 7] 4) [1; 7] |
Функция возрастает на неком промежутке, если на этом промежутке для любых x1>x2, верно, что y(x1)>y(x2).
И наоборот, функция убывает на неком промежутке, если на этом промежутке для любых x1>x2, верно, что y(x1)<y(x2).
Данная функция возрастает на промежутке [3,+∞), следовательно и на промежутке [4; 7] тоже возрастает.
Функция убывает на промежутке (-∞; 3), следовательно и на промежутке [0; 2] тоже убывает.
Остальные промежутки не подходят.
Ответ: А)-3), Б)-1)
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции 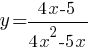 .
.
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Постройте график функции y=(x2+6,25)(x-1)/(1-x) и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 220 миллиметров ртутного столба?
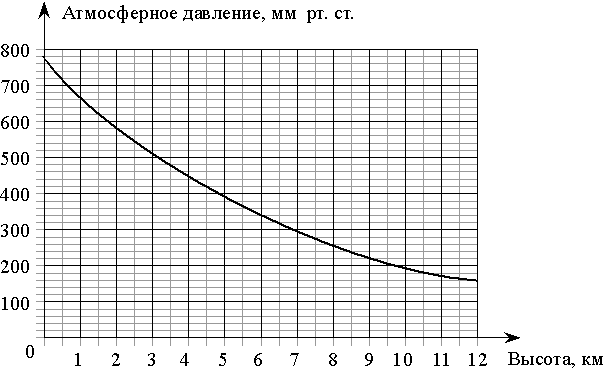
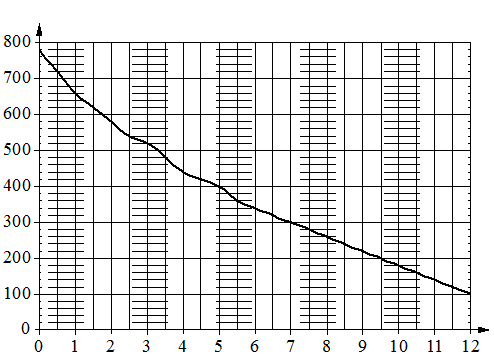 На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, на какой высоте атмосферное давление равно 200 миллиметрам ртутного столба. Ответ дайте в километрах.
На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, на какой высоте атмосферное давление равно 200 миллиметрам ртутного столба. Ответ дайте в километрах.
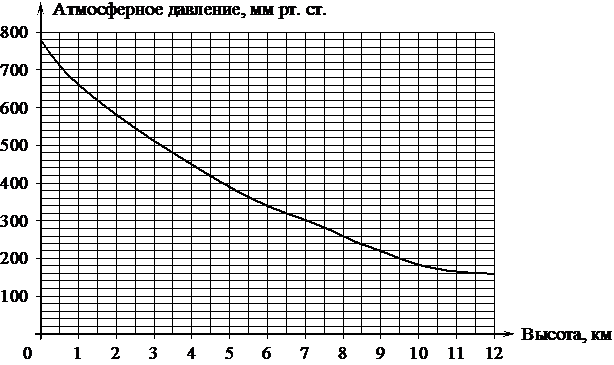 На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). Найдите, чему равно атмосферное давление на высоте 7,5 км. Ответ дайте в миллиметрах ртутного столба.
На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). Найдите, чему равно атмосферное давление на высоте 7,5 км. Ответ дайте в миллиметрах ртутного столба.
Комментарии: