
Постройте график функции
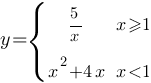 и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
Чтобы построить график этой функции, надо построить график каждой подфункции на указанных для подфункций диапазонах.
y1=5/x на диапазоне [1;+∞)
y2=x2+4x на диапазоне (-∞;1)
График первой подфункции - гипербола, будем строить его просто по точкам:
| X | 1 | 2 | 5 |
| Y | 5 | 2,5 | 1 |
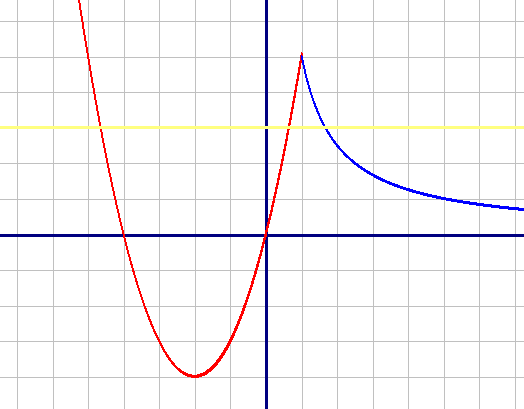 Синим цветом построен график первой подфункции y1=5/x на диапазоне [1;+∞)
Синим цветом построен график первой подфункции y1=5/x на диапазоне [1;+∞)Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции y=x+3|x|-x2 и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
 На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. По горизонтали указана высота над уровнем моря
в километрах, по вертикали — атмосферное давление в миллиметрах ртутного столба. На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 340 миллиметров ртутного столба?
На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. По горизонтали указана высота над уровнем моря
в километрах, по вертикали — атмосферное давление в миллиметрах ртутного столба. На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 340 миллиметров ртутного столба?
Постройте график функции 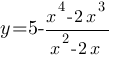 и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Постройте график функции 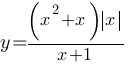 и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
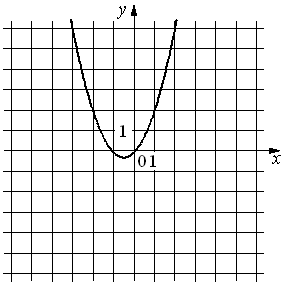 На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
| УТВЕРЖДЕНИЯ | ПРОМЕЖУТКИ |
| А) Функция возрастает на промежутке Б) Функция убывает на промежутке |
1) [-3;3] 2) [0;3] 3) [-3;-1] 4) [-3;0] |
Комментарии:
(2015-05-26 11:43:45) аляска: спасибо огромное!:з