
Постройте график функции 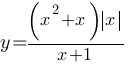 и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
Область Допустимых Значений (ОДЗ):
Так как присутствует деление на (х+1), х≠-1, так как деление на ноль невозможно.
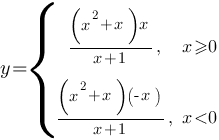
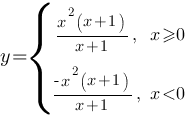
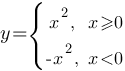
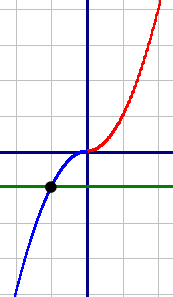 Построим график для каждой подфункции и объединим их.
Построим график для каждой подфункции и объединим их.| X | 0 | 1 | 2 | 3 |
| Y | 0 | 1 | 4 | 9 |
| X | 0 | -1 | -2 |
| Y | 0 | -1 | -4 |
Поделитесь решением
Присоединяйтесь к нам...
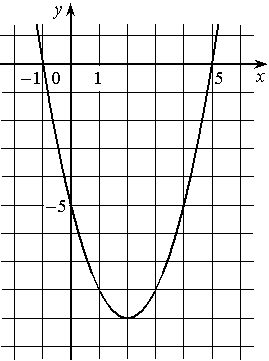 На рисунке изображён график квадратичной функции y=f(x).
На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции являются верными? Запишите их номера.
1) f(-1)=f(5)
2) Функция убывает на промежутке [2; +∞)
3) f(x)>0 при x<-1 и при x>5
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
А) 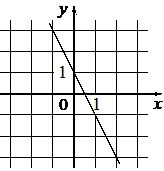 Б)
Б) 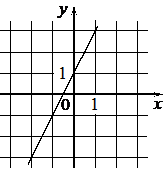 В)
В) 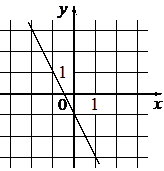
ФОРМУЛЫ
1) y=-2x-1
2) y=-2x+1
3) y=2x+1
В таблице под каждой буквой укажите соответствующий номер.
Постройте график функции y=x2-6|x|-2x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
Установите соответствие между графиками функций и формулами, которые их задают.
| ФОРМУЛЫ | ГРАФИКИ | ||
|
1) y=2/5x+2 2) y=2/5x-2 3) y=-2/5x-2 4) y=-2/5x+2 |
А) 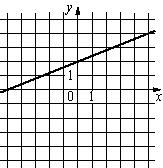 |
Б) 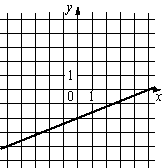 |
В) 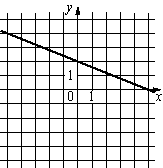 |
 Две прямые пересекаются в точке C (см. рис.). Найдите абсциссу точки C.
Две прямые пересекаются в точке C (см. рис.). Найдите абсциссу точки C.
Комментарии: