
Постройте график функции 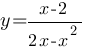 и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Отметим Область допустимых Значений (ОДЗ).
На ноль делить нельзя, следовательно:
2x-x2≠0
x(2-x)≠0
x1≠0
x2≠2
Теперь упростим нашу функцию:
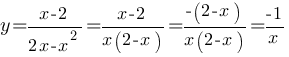
График этой функции - гипербола.
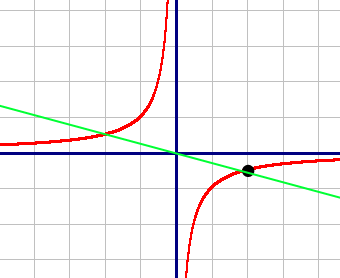 Построим график по точкам:
Построим график по точкам:
| X | -2 | -1 | 1 | 2 |
| Y | 0,5 | 1 | -1 | -0,5 |
Поделитесь решением
Присоединяйтесь к нам...
Одно из чисел 4/7; 6/7; 8/7; 13/7 отмечено на прямой точкой.
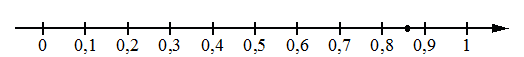
Какое это число?
1) 4/7
2) 6/7
3) 8/7
4) 13/7
На координатной прямой отмечено число a.

Расположите в порядке возрастания числа a-1, 1/a, a.
1) a, 1/a , a-1
2) a, a-1, 1/a
3) a-1, a, 1/a
4) 1/a, a-1, a
На координатной прямой точки A, B, C и D соответствуют числам 0,29; -0,02; 0,109; 0,013.

Какой точке соответствует число 0,109?
1) A
2) B
3) C
4) D
Укажите решение системы неравенств
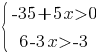
1) 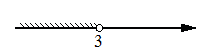
2) 
3) нет решений
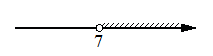
4) 
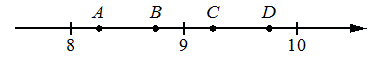 На координатной прямой отмечены точки A, B, C, D. Одна из них соответствует числу √
На координатной прямой отмечены точки A, B, C, D. Одна из них соответствует числу √
1) точка A
2) точка B
3) точка C
4) точка D
Комментарии: