На каком из рисунков изображено решение неравенства x2<9?
1) 
2) 
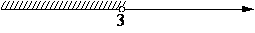
3) 
4) 
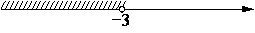
x2<9
x2-9<0
Для решения неравенства
найдем корни
квадратного уравнения
x2-9=0
Можно вычислить через дискриминант, но, в данном случае, можно сделать проще:
x2-32=0
(x-3)(x+3)=0
Произведение равно нулю, когда один из множителей равен нулю, следовательно:
или x-3=0 => x1=3
или x+3=0 => x2=-3
График квадратичной функции - парабола.
Аргумент "а" равен 1, т.е. больше нуля, значит ветви параболы направлены вверх. Корни уравнения - точки пересечения графика функции и оси Х.
Значение функции меньше нуля на диапазоне, где график располагается ниже оси Х, в данном случае (-3;3).
Ответ: 1)
Поделитесь решением
Присоединяйтесь к нам...
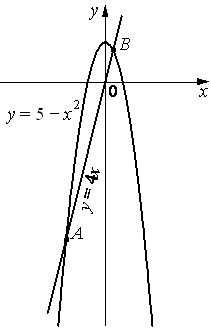На рисунке изображены графики функций y=5-x2 и y=4x. Вычислите абсциссу точки B.
На каком из рисунков изображено решение неравенства 8x-x2≥0?
1) 
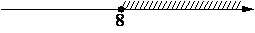
2) 
3) 
4) 
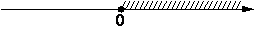
На каком рисунке изображено множество решений системы неравенств
x<3,
4-x>0?
1) 
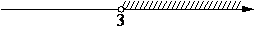
2) 
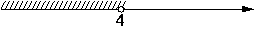
3) 
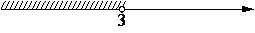
4) 
На координатной прямой отмечено число a.
Расположите в порядке возрастания числа a-1, 1/a, a.
1) a, 1/a , a-1
2) a, a-1, 1/a
3) a-1, a, 1/a
4) 1/a, a-1, a
Решение какого из данных неравенств изображено на рисунке?
1) x2-6x<0
2) x2-6x>0
3) x2-36<0
4) x2-36>0
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: