
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ14 –Η–Ζ 287 |
–ü–Ψ―¹―²―Ä–Ψ–Ι―²–Β –≥―Ä–Α―³–Η–Κ ―³―É–Ϋ–Κ―Ü–Η–Η y=x2-6|x|+2x –Η –Ψ–Ω―Ä–Β–¥–Β–Μ–Η―²–Β, –Ω―Ä–Η –Κ–Α–Κ–Η―Ö –Ζ–Ϋ–Α―΅–Β–Ϋ–Η―è―Ö c –Ω―Ä―è–Φ–Α―è y=c –Η–Φ–Β–Β―² ―¹ –≥―Ä–Α―³–Η–Κ–Ψ–Φ ―Ä–Ψ–≤–Ϋ–Ψ ―²―Ä–Η –Ψ–±―â–Η–Β ―²–Ψ―΅–Κ–Η.
–£ –¥–Α–Ϋ–Ϋ–Ψ–Ι ―³―É–Ϋ–Κ―Ü–Η–Η –Ω―Ä–Η―¹―É―²―¹―²–≤―É–Β–Φ
–Φ–Ψ–¥―É–Μ―¨, ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ ―³―É–Ϋ–Κ―Ü–Η―é –Ϋ–Α–¥–Ψ ―Ä–Α–Ζ–Μ–Ψ–Ε–Η―²―¨ –Ϋ–Α –¥–≤–Β –Ω–Ψ–¥―³―É–Ϋ–Κ―Ü–Η–Η, –≤ –Ζ–Α–≤–Η―¹–Η–Φ–Ψ―¹―²–Η –Ψ―² –Ζ–Ϋ–Α―΅–Β–Ϋ–Η―è
–Φ–Ψ–¥―É–Μ―è:
 x2-6x+2x, –Ω―Ä–Η x≥0
x2-6x+2x, –Ω―Ä–Η x≥0
x2-6(-x)+2x, –Ω―Ä–Η x<0
 x2-4x, –Ω―Ä–Η x≥0
x2-4x, –Ω―Ä–Η x≥0
x2+8x, –Ω―Ä–Η x<0
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ –Η –Ω–Ψ―¹―²―Ä–Ψ–Η–Φ –≥―Ä–Α―³–Η–Κ –¥–Μ―è –Κ–Α–Ε–¥–Ψ–Ι –Ω–Ψ–¥―³―É–Ϋ–Κ―Ü–Η–Η –Η –Ψ–±―ä–Β–¥–Η–Ϋ–Η–Φ –Η―Ö.
1) y1=x2-4x, –Ω―Ä–Η x≥0
| X | 0 | 1 | 2 | 4 |
| Y | 0 | -3 | -4 | 0 |
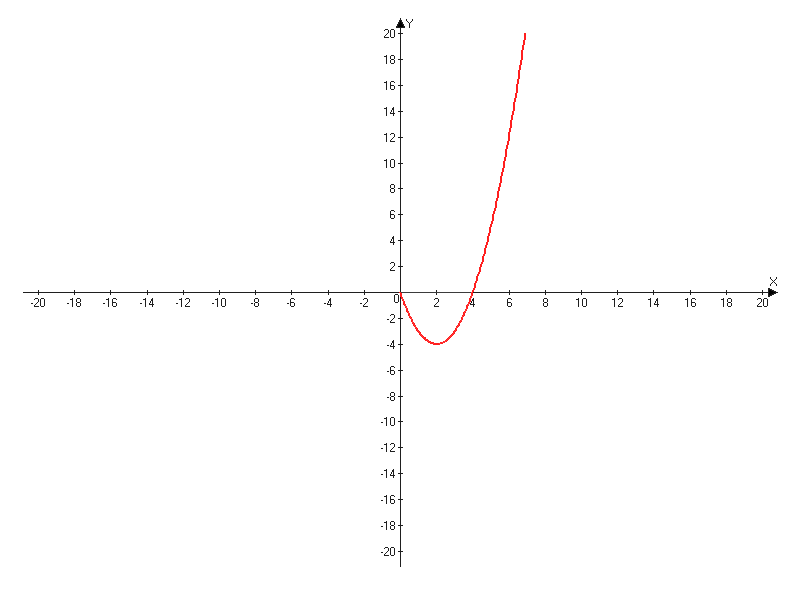
| X | 0 | -1 | -2 | -3 |
| Y | 0 | -7 | -12 | -15 |
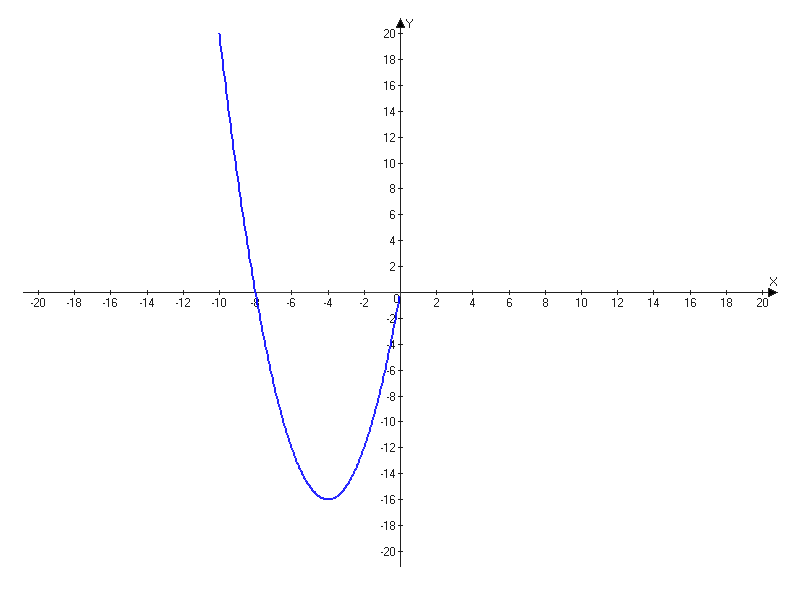
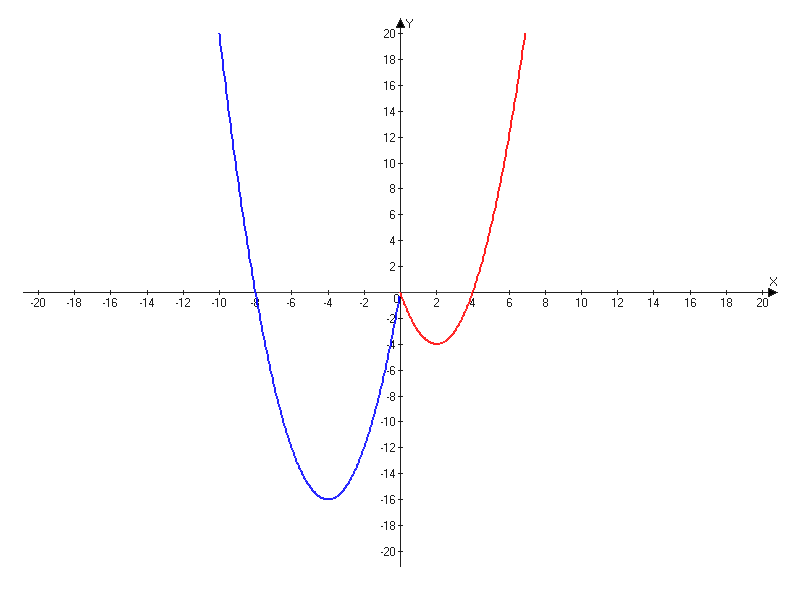
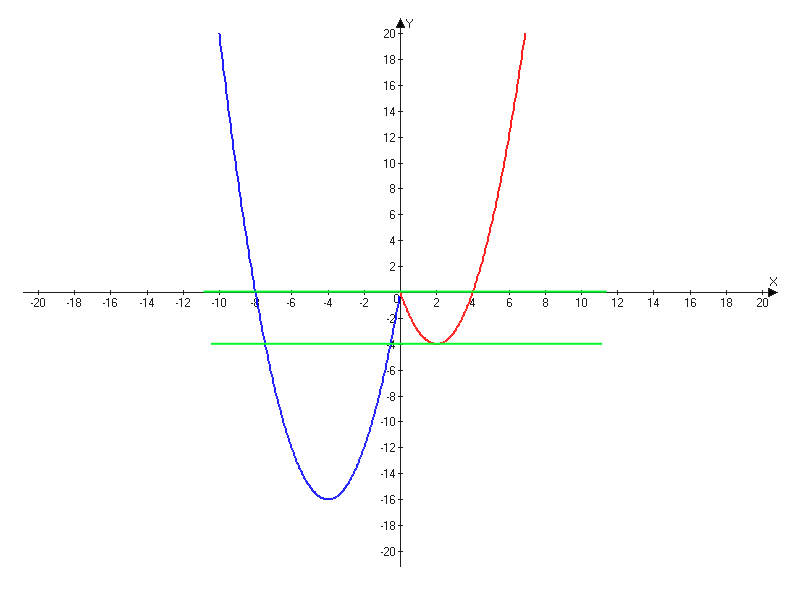
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
–ù–Α ―Ä–Η―¹―É–Ϋ–Κ–Β –Η–Ζ–Ψ–±―Ä–Α–Ε–Β–Ϋ―΄ –≥―Ä–Α―³–Η–Κ–Η ―³―É–Ϋ–Κ―Ü–Η–Ι –≤–Η–¥–Α y=kx+b. –Θ―¹―²–Α–Ϋ–Ψ–≤–Η―²–Β ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Η–Β –Φ–Β–Ε–¥―É –≥―Ä–Α―³–Η–Κ–Α–Φ–Η ―³―É–Ϋ–Κ―Ü–Η–Ι –Η –Ζ–Ϋ–Α–Κ–Α–Φ–Η –Κ–Ψ―ç―³―³–Η―Ü–Η–Β–Ϋ―²–Ψ–≤ k –Η b.
| –ö–û–≠–Λ–Λ–‰–Π–‰–ï–ù–Δ–Ϊ | –™–†–ê–Λ–‰–ö–‰ | ||
|
–ê) k<0, b>0 –ë) k>0, b<0 –£) k<0, b<0 |
1)  |
2)  |
3)  |
–‰–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ –≥―Ä–Α―³–Η–Κ–Η ―³―É–Ϋ–Κ―Ü–Η–Ι y=x2+p –Η y=-2x-2 –Η–Φ–Β―é―² ―Ä–Ψ–≤–Ϋ–Ψ –Ψ–¥–Ϋ―É –Ψ–±―â―É―é ―²–Ψ―΅–Κ―É. –û–Ω―Ä–Β–¥–Β–Μ–Η―²–Β –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―²―΄ ―ç―²–Ψ–Ι ―²–Ψ―΅–Κ–Η. –ü–Ψ―¹―²―Ä–Ψ–Ι―²–Β –≥―Ä–Α―³–Η–Κ–Η –Ζ–Α–¥–Α–Ϋ–Ϋ―΄―Ö ―³―É–Ϋ–Κ―Ü–Η–Ι –≤ –Ψ–¥–Ϋ–Ψ–Ι ―¹–Η―¹―²–Β–Φ–Β –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―².
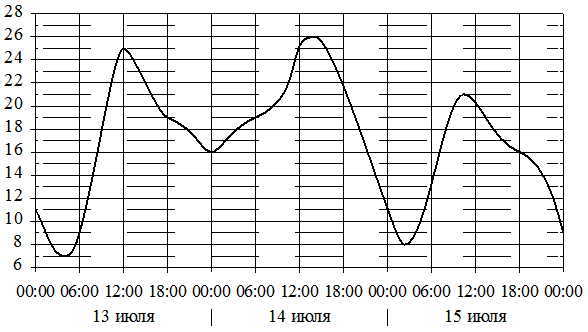 –ù–Α –≥―Ä–Α―³–Η–Κ–Β –Ω–Ψ–Κ–Α–Ζ–Α–Ϋ–Ψ –Η–Ζ–Φ–Β–Ϋ–Β–Ϋ–Η–Β ―²–Β–Φ–Ω–Β―Ä–Α―²―É―Ä―΄ –≤–Ψ–Ζ–¥―É―Ö–Α –Ϋ–Α –Ω―Ä–Ψ―²―è–Ε–Β–Ϋ–Η–Η ―²―Ä―ë―Ö ―¹―É―²–Ψ–Κ. –ü–Ψ –≥–Ψ―Ä–Η–Ζ–Ψ–Ϋ―²–Α–Μ–Η ―É–Κ–Α–Ζ―΄–≤–Α–Β―²―¹―è –¥–Α―²–Α –Η –≤―Ä–Β–Φ―è, –Ω–Ψ –≤–Β―Ä―²–Η–Κ–Α–Μ–Η βÄî –Ζ–Ϋ–Α―΅–Β–Ϋ–Η–Β ―²–Β–Φ–Ω–Β―Ä–Α―²―É―Ä―΄ –≤ –≥―Ä–Α–¥―É―¹–Α―Ö –Π–Β–Μ―¨―¹–Η―è. –û–Ω―Ä–Β–¥–Β–Μ–Η―²–Β –Ω–Ψ –≥―Ä–Α―³–Η–Κ―É –Ϋ–Α–Η–Φ–Β–Ϋ―¨―à―É―é ―²–Β–Φ–Ω–Β―Ä–Α―²―É―Ä―É –≤–Ψ–Ζ–¥―É―Ö–Α 13 –Η―é–Μ―è. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö –Π–Β–Μ―¨―¹–Η―è.
–ù–Α –≥―Ä–Α―³–Η–Κ–Β –Ω–Ψ–Κ–Α–Ζ–Α–Ϋ–Ψ –Η–Ζ–Φ–Β–Ϋ–Β–Ϋ–Η–Β ―²–Β–Φ–Ω–Β―Ä–Α―²―É―Ä―΄ –≤–Ψ–Ζ–¥―É―Ö–Α –Ϋ–Α –Ω―Ä–Ψ―²―è–Ε–Β–Ϋ–Η–Η ―²―Ä―ë―Ö ―¹―É―²–Ψ–Κ. –ü–Ψ –≥–Ψ―Ä–Η–Ζ–Ψ–Ϋ―²–Α–Μ–Η ―É–Κ–Α–Ζ―΄–≤–Α–Β―²―¹―è –¥–Α―²–Α –Η –≤―Ä–Β–Φ―è, –Ω–Ψ –≤–Β―Ä―²–Η–Κ–Α–Μ–Η βÄî –Ζ–Ϋ–Α―΅–Β–Ϋ–Η–Β ―²–Β–Φ–Ω–Β―Ä–Α―²―É―Ä―΄ –≤ –≥―Ä–Α–¥―É―¹–Α―Ö –Π–Β–Μ―¨―¹–Η―è. –û–Ω―Ä–Β–¥–Β–Μ–Η―²–Β –Ω–Ψ –≥―Ä–Α―³–Η–Κ―É –Ϋ–Α–Η–Φ–Β–Ϋ―¨―à―É―é ―²–Β–Φ–Ω–Β―Ä–Α―²―É―Ä―É –≤–Ψ–Ζ–¥―É―Ö–Α 13 –Η―é–Μ―è. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö –Π–Β–Μ―¨―¹–Η―è.
–ü–Ψ―¹―²―Ä–Ψ–Ι―²–Β –≥―Ä–Α―³–Η–Κ ―³―É–Ϋ–Κ―Ü–Η–Η y=2x+4|x|-x2 –Η –Ψ–Ω―Ä–Β–¥–Β–Μ–Η―²–Β, –Ω―Ä–Η –Κ–Α–Κ–Η―Ö –Ζ–Ϋ–Α―΅–Β–Ϋ–Η―è―Ö c –Ω―Ä―è–Φ–Α―è y=c –Η–Φ–Β–Β―² ―¹ –≥―Ä–Α―³–Η–Κ–Ψ–Φ ―Ä–Ψ–≤–Ϋ–Ψ ―²―Ä–Η –Ψ–±―â–Η–Β ―²–Ψ―΅–Κ–Η.
–Θ―¹―²–Α–Ϋ–Ψ–≤–Η―²–Β ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Η–Β –Φ–Β–Ε–¥―É ―³―É–Ϋ–Κ―Ü–Η―è–Φ–Η –Η –Η―Ö –≥―Ä–Α―³–Η–Κ–Α–Φ–Η.
| –ö–û–≠–Λ–Λ–‰–Π–‰–ï–ù–Δ–Ϊ | –™–†–ê–Λ–‰–ö–‰ | |||
|
–ê) y=3x –ë) y=-3x –£) y=(1/3)x |
1) 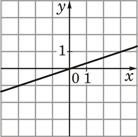 |
2) 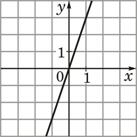 |
3) 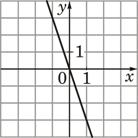 |
4)  |
–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η:
(2017-02-26 17:16:39) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: –¦–Η–¥–Α, –Ω–Ψ―¹–Φ–Ψ―²―Ä–Η―²–Β –Ζ–Α–¥–Α―΅―É β³•121, –Ψ―΅–Β–Ϋ―¨ –Ω–Ψ―Ö–Ψ–Ε–Α –Ϋ–Α –£–Α―à―É.
(2017-02-26 14:34:41) –¦–Η–¥–Α: –ü–Ψ―¹―²―Ä–Ψ–Ι―²–Β –≥―Ä–Α―³–Η–Κ ―³―É–Ϋ–Κ―Ü–Η–Η y=x²-|8x+1| –Η –Ψ–Ω―Ä–Β–¥–Β–Μ–Η―²–Β, –Ω―Ä–Η –Κ–Α–Κ–Η―Ö –Ζ–Ϋ–Α―΅–Β–Ϋ–Η―è―Ö m –Ω―Ä―è–Φ–Α―è y=m –Η–Φ–Β–Β―² ―¹ –≥―Ä–Α―³–Η–Κ–Ψ–Φ ―Ä–Ψ–≤–Ϋ–Ψ ―²―Ä–Η –Ψ–±―â–Η–Β ―²–Ψ―΅–Κ–Η.
(2015-05-21 20:38:16) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: –Λ–Α―è, –Ω–Ψ―΅–Β–Φ―É –Ψ–±–Μ–Α―¹―²―¨? –Δ–Ψ–Μ―¨–Κ–Ψ –Ω―Ä–Η ―¹=0 –Η ―¹=-4 –±―É–¥–Β―² ―Ä–Ψ–≤–Ϋ–Ψ ―²―Ä–Η –Ψ–±―â–Η–Β ―²–Ψ―΅–Κ–Η, –Α –≤ –Ψ–±–Μ–Α―¹―²–Η (-4;0) –±―É–¥–Β―² 4 ―²–Ψ―΅–Κ–Η.
(2015-05-20 16:01:12) –Λ–Α―è: –Ψ―²–≤–Β―² ―¹ –Ω―Ä–Η–Ϋ–Α–¥–Μ–Β–Ε–Η―² –Ψ–±–Μ–Α―¹―²―¨ –Ψ―² 0 –¥–Ψ -4!