В треугольнике ABC проведена биссектриса AL, угол ALC равен 145°, угол ABC равен 113°. Найдите угол ACB. Ответ дайте в градусах.
Пусть ∠BAL=x
Тогда, ∠LAC тоже =x (так как AL -
биссектриса).
Рассмотрим треугольник ABC:
∠ABC+∠ACB+∠CAB=180° (по
теореме о сумме углов треугольника).
113°+∠ACB+2x=180°
∠ACB+2x=67°
x=(67°-∠ACB)/2
Рассмотрим треугольник ALC:
∠ALC+∠ACB+∠LAC=180° (по
теореме о сумме углов треугольника).
145°+∠ACB+x=180°
∠ACB+x=35°
Подставляем значение x, полученное ранее:
∠ACB+(67°-∠ACB)/2=35° |*2
2∠ACB+67°-∠ACB=70°
∠ACB+67°=70°
∠ACB=70°-67°=3°
Ответ: 3
Поделитесь решением
Присоединяйтесь к нам...
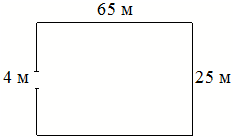Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 25 м и 65 м. Найдите длину забора (в метрах), которым нужно огородить участок, предусмотрев проезд шириной 4 м.
Два ребра прямоугольного параллелепипеда равны 8 и 5,
а объём параллелепипеда равен 280. Найдите площадь поверхности этого параллелепипеда.
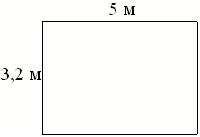На плане указано, что прямоугольная комната имеет площадь 15,7 кв. м. Точные измерения показали, что ширина комнаты равна 3,2 м, а длина 5 м.
На сколько квадратных метров площадь комнаты отличается от значения, указанного на плане?
Найдите площадь ромба, если его высота равна 6, а острый угол равен 30°.
Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 17. Найдите площадь боковой поверхности этой пирамиды.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: