
 Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 17. Найдите площадь боковой поверхности этой пирамиды.
Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 17. Найдите площадь боковой поверхности этой пирамиды.
Площадь боковой поверхности пирамиды равна сумме боковых граней пирамиды, которые являются равными треугольниками со сторонами 16, 17 и 17.
Площадь такого треугольника легче вычислить через три стороны (формула Герона).
Полупериметр:
p=(16+17+17)/2=50/2=25
S=√p(p-a)(p-b)(p-c)=√25(25-16)(25-17)(25-17)=√25*9*8*8=
По свойству арифметического корня:
=√25*√9*√8*8=5*3*8=120
Это площадь одной боковой грани, значит площадь всей боковой поверхности:
Sбп=3*S=3*120=360
Ответ: 360
Поделитесь решением
Присоединяйтесь к нам...
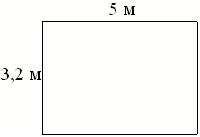 На плане указано, что прямоугольная комната имеет площадь 15,7 кв. м. Точные измерения показали, что ширина комнаты равна 3,2 м, а длина 5 м.
На сколько квадратных метров площадь комнаты отличается от значения, указанного на плане?
На плане указано, что прямоугольная комната имеет площадь 15,7 кв. м. Точные измерения показали, что ширина комнаты равна 3,2 м, а длина 5 м.
На сколько квадратных метров площадь комнаты отличается от значения, указанного на плане?
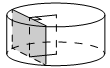 Радиус основания цилиндра равен 15, а его образующая
равна 14. Сечение, параллельное оси цилиндра, удалено
от неё на расстояние, равное 12. Найдите площадь этого сечения.
Радиус основания цилиндра равен 15, а его образующая
равна 14. Сечение, параллельное оси цилиндра, удалено
от неё на расстояние, равное 12. Найдите площадь этого сечения.
 Аквариум имеет форму прямоугольного параллелепипеда
с размерами 80 см x 30 см x 40 см. Сколько литров составляет объём аквариума?
Аквариум имеет форму прямоугольного параллелепипеда
с размерами 80 см x 30 см x 40 см. Сколько литров составляет объём аквариума?
В одном литре 1000 кубических сантиметров.
 На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
 Радиус основания цилиндра равен 15, а его образующая
равна 14. Сечение, параллельное оси цилиндра, удалено
от неё на расстояние, равное 12. Найдите площадь этого сечения.
Радиус основания цилиндра равен 15, а его образующая
равна 14. Сечение, параллельное оси цилиндра, удалено
от неё на расстояние, равное 12. Найдите площадь этого сечения.
Комментарии: