
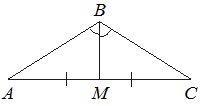
 В треугольнике ABC угол B равен 120°. Медиана BM делит угол B пополам и равна 27. Найдите длину стороны AB.
В треугольнике ABC угол B равен 120°. Медиана BM делит угол B пополам и равна 27. Найдите длину стороны AB.
Так как медиана делит угол пополам, то она так же является и
биссектрисой. Одновременно быть и
биссектрисой и медианой отрезок может только в равнобедренном треугольнике (по
свойству равнобедренного треугольника), тогда этот отрезок так же является и
высотой.
Т.е. треугольник ABM - прямоугольный.
∠ABM=∠B/2=120°/2=60°
Так как ABM прямоугольный, то по определению косинуса:
cos∠ABM=BM/AB
cos60°=27/AB (cos60°=1/2 по таблице)
1/2=27/AB |*2
1=54/AB
AB=54
Ответ: 54
Поделитесь решением
Присоединяйтесь к нам...
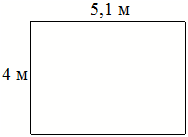 На плане указано, что прямоугольная комната имеет площадь 20,1 кв. м. Точные измерения показали, что ширина комнаты равна 4 м,
а длина 5,1 м. На сколько квадратных метров площадь комнаты отличается от площади, указанной на плане?
На плане указано, что прямоугольная комната имеет площадь 20,1 кв. м. Точные измерения показали, что ширина комнаты равна 4 м,
а длина 5,1 м. На сколько квадратных метров площадь комнаты отличается от площади, указанной на плане?
Найдите площадь ромба, если его высота равна 6, а острый угол равен 30°.
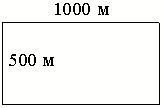 Участок земли под строительство санатория имеет форму прямоугольника, стороны которого равны 1000 м и 500 м. Одна из больших сторон участка идёт вдоль моря, а три остальные стороны нужно оградить забором. Найдите длину этого забора. Ответ дайте
в метрах.
Участок земли под строительство санатория имеет форму прямоугольника, стороны которого равны 1000 м и 500 м. Одна из больших сторон участка идёт вдоль моря, а три остальные стороны нужно оградить забором. Найдите длину этого забора. Ответ дайте
в метрах.
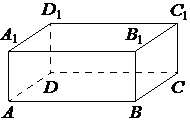 В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра DA, DC и диагональ DA1 боковой грани равны соответственно 3, 5 и √
В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра DA, DC и диагональ DA1 боковой грани равны соответственно 3, 5 и √
 Участок земли под строительство санатория имеет форму прямоугольника, стороны которого равны 1000 м и 500 м. Одна из больших сторон участка идёт вдоль моря, а три остальные стороны нужно оградить забором. Найдите длину этого забора. Ответ дайте
в метрах.
Участок земли под строительство санатория имеет форму прямоугольника, стороны которого равны 1000 м и 500 м. Одна из больших сторон участка идёт вдоль моря, а три остальные стороны нужно оградить забором. Найдите длину этого забора. Ответ дайте
в метрах.
Комментарии: