
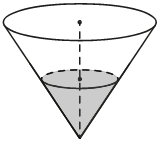
 В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём сосуда 1600 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.
В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём сосуда 1600 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.
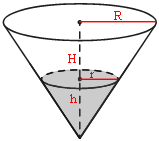 Рассмотрим треугольники, которые образуют:
Рассмотрим треугольники, которые образуют:
1) R-радиус основания сосуда, H-высота сосуда и боковая сторона сосуда
2) r-радиус конуса, образованный жидкостью, h-высота этого же конуса и боковая сторона этого конуса
Нижний угол этих треугольников общий.
Углы, образованные радиусами и высотами, прямые.
Следовательно, по первому признаку подобия треугольников эти треугольники
подобны.
Тогда, мы можем записать:
H/h=R/r
Из условия нам известно, что h=H/2, следовательно r=R/2.
Так как сосуд имеет вид конуса, то его объем мы можем записать так:
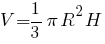
Соответственно, объем жидкости, которая тоже имеет форму конуса, мы запишем так:
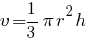
Подставляем значения r и h, выраженные через R и H.
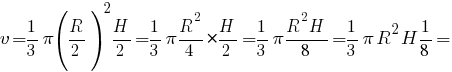
Заметим, все весь результат, кроме 1/8, это объем сосуда, т.е. можем записать:
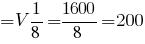
Ответ: 200
Поделитесь решением
Присоединяйтесь к нам...
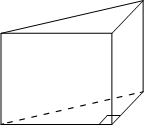 В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 3,
а гипотенуза равна √
В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 3,
а гипотенуза равна √
В параллелограмме ABCD диагонали делят его углы пополам и равны 40 и 42. Найдите периметр параллелограмма ABCD.
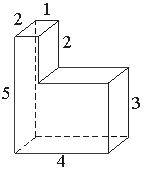 Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа
на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа
на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
На координатной прямой отмечены точки A, B, C и D.

Число m равно √2.
Установите соответствие между указанными точками и числами в правом столбце, которые им соответствуют.
| ТОЧКИ | ЧИСЛА |
| A | 1) 2m-5 |
| B | 2) m3 |
| C | 3) m-1 |
| D | 4) -1/m |
Найдите площадь ромба, если его высота равна 6, а острый угол равен 30°.
Комментарии: