Решение какого из данных неравенств изображено на рисунке?
1) x2-36≤0
2) x2+36≤0
3) x2-36≥0
4) x2+36≥0
Посмотрим на предложенные неравенства:
- все они квадратичные, т.е. графики этих функций - параболы
- у всех аргумент "а" равен единице, т.е. больше нуля, следовательно ветви их парабол направлены вверх
- графики парабол 1) и 3) будут совпадать, т.к. это одинаковые функции.
- графики парабол 2) и 4) будут совпадать, т.к. это одинаковые функции.
Посмотрим на рисунок решения неравенства:
- корни квадратичной функции должны быть -6 и 6.
Решим уравнение x2-36=0
x2-62=0
(x-6)(x+6)=0
x-6=0 => x1=6
x+6=0 => x2=-6
Неравенства 1) и 3), судя по корням, подходят.
Решим уравнение x2+36=0
x2=-36
Данное уравнение не имеет корней, т.к. ни какое число, возведенное в квадрат не даст отрицательный результат. Значит неравенства 2) и 4) не подходят.
Посмотрим на рисунок, в условии показан диапазон, когда график функции ниже оси Х, т.е. меньше нуля, следовательно, подходит неравенство x2-36≤0
Ответ: 1)
Поделитесь решением
Присоединяйтесь к нам...
На рисунке изображены графики функций вида y=kx+b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
КОЭФФИЦИЕНТЫ
А) k<0, b>0
Б) k<0, b<0
В) k>0, b<0
ГРАФИКИ
1) 
2) 
3) 
На координатной прямой отмечены точки A, B, C, D. Одна из них соответствует числу √
1) точка A
2) точка B
3) точка C
4) точка D
На координатной прямой отмечено число a.
Расположите в порядке возрастания числа a-1, 1/a, a.
1) a, 1/a , a-1
2) a, a-1, 1/a
3) a-1, a, 1/a
4) 1/a, a-1, a
На каком рисунке изображено множество решений неравенства x-1≤3x+2?
1) 
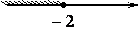
2) 
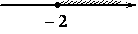
3) 
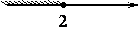
4) 
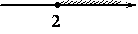
На координатной прямой отмечены числа а и с.
Какое из следующих утверждений неверно?
1) c-a<0
2) ac>0
3) 0<c+1<1
4) -a>0
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: