Автор: ТаськаНа координатной прямой отмечены числа b и с.
Какое из следующих чисел наименьшее?
1) b+c
2) 2c
3) -b
4) bc
Как видно из координатной прямой, числа b и c - отрицательные, следовательно:
1) b+c - будет тоже отрицательным.
2) 2c - отрицательное.
3) -b - будет положительным, так как минус на минус дает плюс.
4) bc - тоже будет положительным, так как произведение двух отрицательных чисел дает положительный результат.
Следовательно, 3) и 4) не могут быть наименьшими.
Расположим числа b+c и 2c на координатной прямой.
"2c" от нуля располагается на расстоянии вдвое большем, чем "с".
"b+c" располагается от "b" на расстоянии, как "с" от нуля.
Получается, что наименьшее - "b+c".
Ответ: 1)
Поделитесь решением
Присоединяйтесь к нам...
На координатной прямой отмечены точки A, B, C, D. Одна из них соответствует числу √
Какая это точка?
1) точка A
2) точка B
3) точка C
4) точка D
На координатной прямой отмечены числа а и с.
Какое из следующих утверждений неверно?
1) a-c>0
2) -3<a+1<-2
3) a/c<0
4) -c>-1
Постройте график функции 
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
На координатной прямой точки A, B, C и D соответствуют числам 0,29; -0,02; 0,109; 0,013.
Какой точке соответствует число 0,109?
1) A
2) B
3) C
4) D
На каком рисунке изображено множество решений неравенства x2-17x+72≥0?
1) 
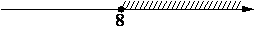
2) 
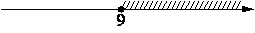
3) 
4) 
Хочу получать новые решения
Ни какого спама
Комментарии: