
Установите соответствие между функциями и их графиками.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | |||
|
А) y=-2x+4 Б) y=2x-4 В) y=2x+4 |
1) 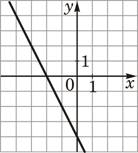 |
2) 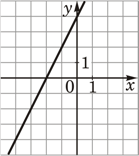 |
3) 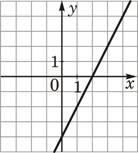 |
4) 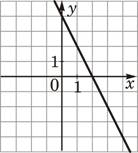 |
Общий вид функции прямой можно представить в виде y=kx+b.
Если прямая слева направо возрастает, то k>0 (как на графиках 2) и 3)), и наоборот, если прямая слева направо убывает, то k<0 (как на графиках 1) и 4)).
Узнать знак коэффициента b, можно приравняв х к нулю. Получим: y=k*0+b=b. Посмотрим на график и узнаем b больше нуля или меньше. Т.е коэффициент b - это координата "y" точки пересечения прямой и оси y. Тогда:
1) Для первого графика k<0, а b=-4. Нет соответствующей функции.
2) Для второго графика k>0, а b=4. Соответствует функции В).
3) Для третьего графика k>0, а b=-4. Соответствует функции Б).
4) Для четвертого графика k<0, а b=4. Соответствует функции А).
Ответ: А) - 4), Б) - 3), В) - 2)
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции 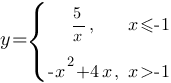 и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
Постройте график функции y=x2-|6x+7|.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Установите соответствие между графиками функций и формулами, которые их задают.
| ФОРМУЛЫ | ГРАФИКИ | ||
|
1) y=2/5x+2 2) y=2/5x-2 3) y=-2/5x-2 4) y=-2/5x+2 |
А) 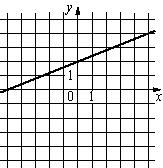 |
Б) 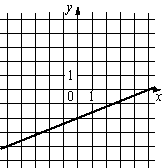 |
В) 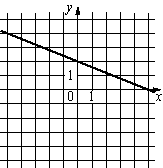 |
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
КОЭФФИЦИЕНТЫ
А) k<0, b<0
Б) k<0, b>0
В) k>0, b<0
ГРАФИКИ
1)  2)
2)  3)
3) 
В таблице под каждой буквой укажите соответствующий номер.
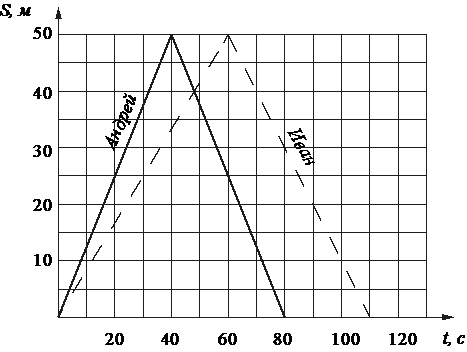 Андрей и Иван соревновались в 50-метровом бассейне на дистанции 100 м. Графики их заплывов показаны на рисунке. По горизонтальной оси отложено время, а по вертикальной – расстояние пловца от старта. Кто выиграл соревнование? В ответе запишите, на сколько секунд он обогнал соперника.
Андрей и Иван соревновались в 50-метровом бассейне на дистанции 100 м. Графики их заплывов показаны на рисунке. По горизонтальной оси отложено время, а по вертикальной – расстояние пловца от старта. Кто выиграл соревнование? В ответе запишите, на сколько секунд он обогнал соперника.
Комментарии: