Постройте график функции y=x2-|6x+7|.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
В данной функции присутствует модуль, следовательно функцию надо разложить на две функции, в зависимости от значения модуля:
y1=x2-(6x+7), при 6x+7≥0
y2=x2-(-(6x+7)), при 6x+7<0
y1=x2-6x-7, при x≥-7/6
y2=x2+6x+7, при x<-7/6
График обеих подфункций - парабола, у обеих подфункций коэффициент "а" равен 1, т.е. больше нуля. Следовательно, ветви обеих парабол направлены вверх.
Построим по точкам графики обеих подфункций, но первый график на диапазоне от -7/6 до +∞, а второй график на диапазоне от -∞ до -7/6 (как указано для подфункций).
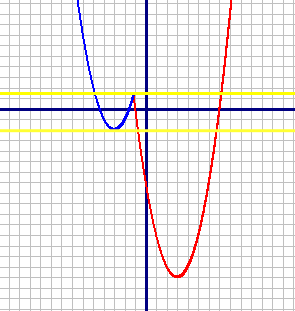Подфункция y1=x2-6x-7 (Красный график)
| X | -1 | 0 | 1 | 2 | 3 |
| Y | 0 | -7 | -12 | -15 | -16 |
| X | -2 | -3 | -4 | -5 |
| Y | -1 | -2 | -1 | 2 |
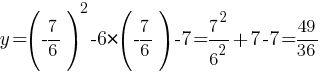, т.е. и m1=49/36.Поделитесь решением
Присоединяйтесь к нам...
Две прямые пересекаются в точке C (см. рис.). Найдите абсциссу точки C.
Постройте график функции
y=3|x+7|-x2-13x-42.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
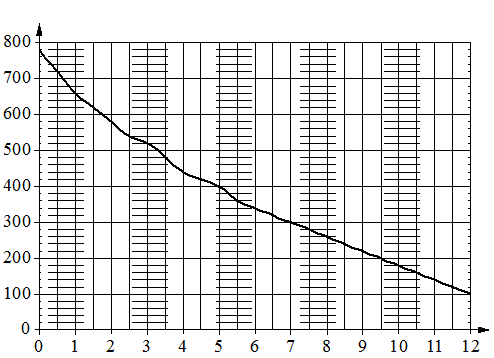На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, на какой высоте атмосферное давление равно 620 миллиметрам ртутного столба. Ответ дайте в километрах.
Постройте график функции y=x+3|x|-x2 и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
Постройте график функции
y=3|x+7|-x2-13x-42.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: