Постройте график функции
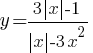
Определите, при каких значениях k прямая y=kx не имеет с графиком общих точек.
В данной функции присутствуем
модуль, следовательно функцию надо разложить на две подфункции, в зависимости от значения
модуля:
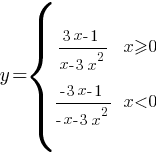
Теперь надо построить график каждой подфункции в его границах и объединить их.
1) 
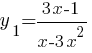, при х≥0.
Напишем Область Допустимых Значений (ОДЗ).
Так как знаменатель не может равняться нулю, то x-3x2≠0 Следовательно:
x(1-3x)≠0
x1≠0
x2≠1/3
Теперь можно упростить равенство:
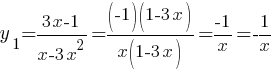
График представляет из себя гиперболу, отметим несколько точек:
| X | 0,5 | 1 | 2 |
| Y | -2 | -1 | -0,5 |
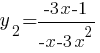, при х<0.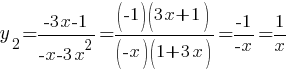
| X | -0,5 | -1 | -2 |
| Y | -2 | -1 | -0,5 |
График первой подфункции начерчен красным цветом, второй подфункции - синим.Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции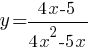 
.
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Установите соответствие между графиками функций и формулами, которые их задают.
| ФОРМУЛЫ | ГРАФИКИ | ||
|
1) y=-x/2-1 2) y=-x/2+1 3) y=x/2+1 |
А)  |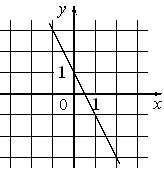
Б)  |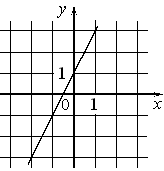
В)  |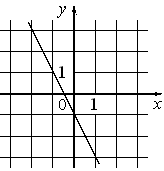
Постройте график функции y=4|x+6|-x2-11x-30 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Постройте график функции y=x2-5|x|+4. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
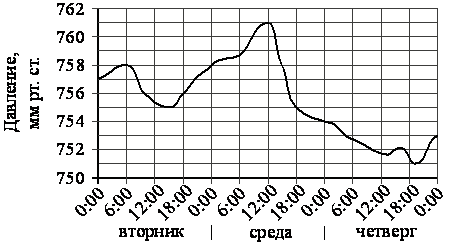На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели и время, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите значение атмосферного давления во вторник в 18 часов.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: