Найдите наименьшее значение x, удовлетворяющее системе неравенств
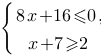
Для решения этой задачи надо решить систему неравенств и найти наименьшее значение х из этого решения.
Чтобы решить систему неравенств, необходимо:
1) решить каждое неравенство по отдельности. Решением неравенства является диапазон, удовлетворяющий неравенству.
2) наложить полученные диапазоны друг на друга. Новые диапазоны, полученные при пересечение исходных и будут решением системы неравенств.
Приступим:
1) Первое неравенство:
8x+16≤0
8x≤-16 |:8
x≤-2
Т.е. решение первого неравенства x⊂(-∞;-2].
Второе неравенство:
x+7≥0
x≥-7
Т.е. решение второго неравенства x⊂[-7;+∞).
2) При пересечении решений, получаем диапазон [-7;-2].
Очевидно, что наименьшее значение - это -7.
Ответ: -7
Поделитесь решением
Присоединяйтесь к нам...
Укажите решение неравенства -3-x≥4x+7.
1) (-∞; -0,8)
2) (-∞; -2)
3) (-2; +∞)
4) (-0,8; +∞)
Смешали некоторое количество 11-процентного растворанекоторого вещества с таким же количеством 81-процентного раствораэтого же вещества. Сколько процентов составляет концентрация получившегося раствора?
На счёт в банке, доход по которому составляет 20% годовых, внесли 29 тыс. руб.. Сколько тысяч рублей будет на этом счёте через год, если никаких операций, кроме начисления процентов, со счётом проводиться не будет?
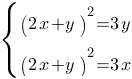
Найдите корень уравнения 8-5(2x-3)=13-6x.
Первые 300 км автомобиль ехал со скоростью 60 км/ч, следующие 300 км — со скоростью 100 км/ч, а последние 300 км — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Хочу получать новые решения
Ни какого спама
Автор: Таська
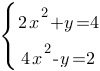
Комментарии: