
Туристы проплыли на лодке от лагеря некоторое расстояние вверх по течению реки, затем причалили к берегу и, погуляв 3 часа, вернулись обратно через 5 часов от начала путешествия. На какое расстояние от лагеря они отплыли, если скорость течения реки равна 3 км/ч, а собственная скорость лодки 6 км/ч?
Обозначим:
S - расстояние от лагеря до места прогулки.
t1 - время движения лодки против течения.
t2 - время движения лодки по течению.
Скорость лодки против течения равна 6-3=3 км/ч.
Скорость лодки по течению - 6+3=9 км/ч
Составим уравнения:
Движение лодки против течения:
S=3t1
Движение лодки по течению:
S=9t2
Время в поездке:
5=t1+t2+3
t1=2-t2
 S=3(2-t2)
S=3(2-t2)
S=9t2
Так как S в обоих уравнениях это одно и то же расстояние, то:
3(2-t2)=9t2
Сократим правую и левую части уравнения на 3:
2-t2=3t2
2=4t2
t2=2/4=0,5 часа.
Подставляем во второе уравнение:
S=9t2=9*0,5=4,5 км.
Ответ: 4,5
Поделитесь решением
Присоединяйтесь к нам...
Решите неравенство (2x-7)2≥(7x-2)2.
Расстояние между двумя пристанями по реке равно 24 км. Моторная лодка прошла от одной пристани до другой, сделала стоянку на 1 ч 40 мин и вернулась обратно. Всё путешествие заняло 6 целых и 2/3 ч. Найдите скорость течения реки, если известно, что скорость моторной лодки в стоячей воде равна 10 км/ч.
Решите неравенство 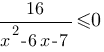
Укажите решение неравенства 5x-2(2x-8)<-5.
1) (-∞;11)
2) (11;+∞)
3) (-∞;-21)
4) (-21;+∞)
Решите уравнение x2+2x-15=0.
Комментарии: