Парабола проходит через точки K(0;-5), L(4;3), M(-3;10). Найдите координаты её вершины.
Парабола - это график для квадратичной функции вида:
y=ax2+bx+c
Чтобы найти координаты вершины параболы (x0;y0), надо определить саму функцию, т.е. найти коэффициенты а, b и c.
Подставляем координаты точек в функцию для каждой точки:
K: -5=a*02+b*0+c
L: 3=a*42+b*4+c
M: 10=a*(-3)2+b*(-3)+c
И объединим эти уравнения в систему:
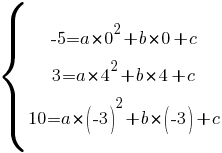
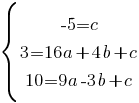
В первом равенстве мы сразу узнали значение "с", подставляем его в другие два уравнения:
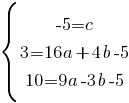
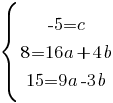
Для упрощения вычислений, разделим правую и левую части уравнений, второе уравнение на 4, а третье на 3:
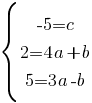
Преобразуем второе уравнение так, чтобы в левой части осталось только "b", а в правой части все остальное:
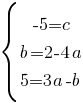
И подставим полученное значение "b" в третье уравнение:
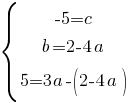
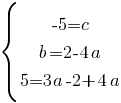
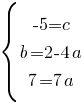
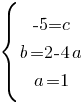
Подставляем значение "а" во второе уравнение:
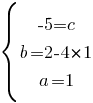
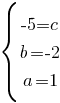
Т.е. мы получили функцию:
y=x2-2x-5
x0=-b/(2a)=-(-2)/(2*1)=2/2=1
y0=x02-2x0-5=102-2*10-5=1-2-5=-6
Ответ: (1;-6)
Поделитесь решением
Присоединяйтесь к нам...
Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой tF=1,8tC+32, где tC — температура в градусах Цельсия, tF — температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует 50 градусов по шкале Цельсия?
Найдите значение выражения √
1) 28
2) 4√
3) 4
4) 16√
Решите уравнение (x-2)2(x-3)=12(x-2).
За 5 минут пешеход прошёл a метров. За сколько минут он пройдёт 120 метров, если будет идти с той же скоростью? Запишите соответствующее выражение.
Какое из данных ниже чисел является значением выражения √18*80*√30?
1) 360
2) 120√15
3) 120√6
4) 120√3
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: