
Расстояние между двумя пристанями по реке равно 24 км. Моторная лодка прошла от одной пристани до другой, сделала стоянку на 1 ч 40 мин и вернулась обратно. Всё путешествие заняло 6 целых и 2/3 ч. Найдите скорость течения реки, если известно, что скорость моторной лодки в стоячей воде равна 10 км/ч.
Первое: 6 целых и 2/3 ч. - это 6 часов 40 минут.
Второе: если лодка идет по течению реки, то ее скорость складывается со скоростью реки, а если против течения, то вычитается.
Обозначим:
скорость реки - v
Время лодки в пути по течению - t1
Время лодки в пути против течения - t2
Движение лодки по течению (1):
24=(10+v)t1
Движение лодки против течения (2):
24=(10-v)t2
При этом, время в пути составило t1+t2, и равно это 6 часов 40 минут минус 1 час 40 мин (на стоянку) и равно это 5 часов (3).
(1) t1=24/(10+v)
(2) t2=24/(10-v)
Подставляем в (3):
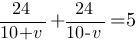
Приводим к общему знаменателю:
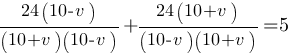
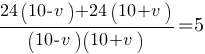
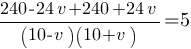
В знаменателе применим формулу
разность квадратов:
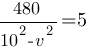
480=5*(100-v2)
480=500-5v2
5v2=500-480
5v2=20
v2=4
v=2 км/ч
Ответ: 2
Поделитесь решением
Присоединяйтесь к нам...
Укажите неравенство, решением которого является любое число.
1) x2+70>0
2) x2-70>0
3) x2+70<0
4) x2-70<0
Решите неравенство 5x-2(2x-8)<-5.
1) (-∞;11)
2) (11;+∞)
3) (-∞;-21)
4) (-21;+∞)
На каком рисунке изображено множество решений системы неравенств
 3+3x<0,
3+3x<0,
2-3x<14?
1) система не имеет решений
2) 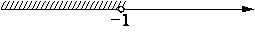
3) 
4) 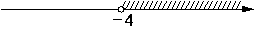
Решите неравенство 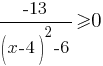
Два велосипедиста одновременно отправляются в 60-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.
Комментарии: