
Укажите неравенство, решением которого является любое число.
1) x2+70>0
2) x2-70>0
3) x2+70<0
4) x2-70<0
В данном случае нет необходимости решать эти неравенства. Рассмотрим неравенства и будем рассуждать логически:
1) x2+70>0
x2 - это всегда положительное число при любом "х". Следовательно, положительное число + другое положительное число (70) тоже всегда положительное, т.е. больше нуля.
Получается, что это и есть ответ на эту задачу.
Но для общего развития рассмотрим и остальные неравенства.
2) x2-70>0
x2>70
Очевидно, что найдутся такие "х", которые не удовлетворяют неравенству, например 1:
12>70 - не верно. Т.е. это не ответ на задачу.
3) x2+70<0
В п.1 мы выяснили, что при любом "х" x2+70 будет больше нуля, следовательно неравенство x2+70<0 вообще не имеет решений.
4) x2-70<0
4) x2<70
Найдутся такие "х", которые не удовлетворяют данному неравенству, например 10:
102<70
100<70 - не верно.
Ответ: 1)
Поделитесь решением
Присоединяйтесь к нам...
Найдите корень уравнения 4(x-8)=-5.
Решите уравнение 3x2-7x+29=(x+4)2.
Решите уравнение 1/(x-2)2-1/(x-2)-6=0
Решите систему уравнений 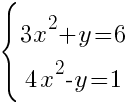
Решите уравнение x3+5x2-9x-45=0.
Комментарии: