
 Две прямые пересекаются в точке C (см. рис.). Найдите абсциссу точки C.
Две прямые пересекаются в точке C (см. рис.). Найдите абсциссу точки C.
Пересечение двух графиков означает, что эти графики имеют общую точку. Т.е. обе функции имеют общую точку. И чтобы найти ее надо обе функции объединить в систему и решить ее:
 2x-y=-1
2x-y=-1
x+3y=10
 2x+1=y (Подставляем это значение "y" во второе уравнение)
2x+1=y (Подставляем это значение "y" во второе уравнение)
x+3(2x+1)=10
 2x+1=y
2x+1=y
x+6x+3=10
 2x+1=y
2x+1=y
7x=10-3
 2x+1=y
2x+1=y
x=1 (подставляем это значение в первое уравнение)
 2*1+1=y
2*1+1=y
x=1
 y=3
y=3
x=1
Решение системы (1;3) - это координаты точки пересечения графиков (точка С), следовательно, абсцисса точки С равна 1, а ордината равна 3.
Ответ: 1
Поделитесь решением
Присоединяйтесь к нам...
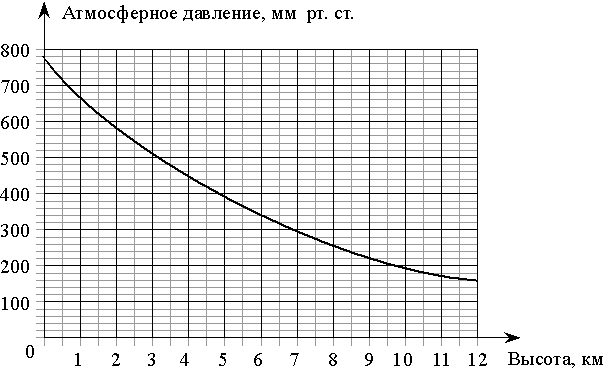 На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 580 миллиметров ртутного столба?
На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 580 миллиметров ртутного столба?
Постройте график функции y=(x2+6,25)(x-1)/(1-x) и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Постройте график функции
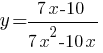 .
.
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
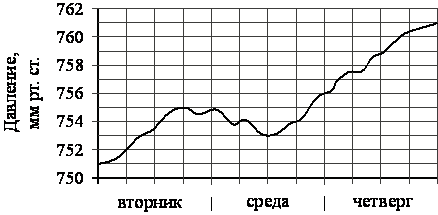 На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наименьшее значение атмосферного давления в среду (мм рт. ст.).
На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наименьшее значение атмосферного давления в среду (мм рт. ст.).
На рисунке изображены графики функций вида y=ax2+bx+c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | ||
|
1) a<0, c<0 2) a>0, c>0 3) a>0, c<0 4) a<0, c>0 |
А)  |
Б)  |
В)  |
Комментарии: