
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
КОЭФФИЦИЕНТЫ
А) k<0, b<0
Б) k<0, b>0
В) k>0, b<0
ГРАФИКИ
1)  2)
2)  3)
3) 
В таблице под каждой буквой укажите соответствующий номер.
Если прямая слева направо возрастает, то k>0 (как на графике 1)), и наоборот, если прямая слева направо убывает, то k<0 (как на графиках 2) и 3)).
Узнать знак коэффициента b, можно приравняв х к нулю. Получим: y=k*0+b=b.
Посмотрим на график и узнаем b больше нуля или меньше. Т.е если прямая пересекает ось Y ниже оси X, то b - отрицательная, если выше - положительная. Тогда:
Для графика 1): k>0, b<0 - вариант В)
Для графика 2): k<0, b<0 - вариант А)
Для графика 3): k<0, b>0 - вариант Б)
| ГРАФИКИ | А) | Б) | В) |
| КОЭФФИЦИЕНТЫ | 2) | 3) | 1) |
Поделитесь решением
Присоединяйтесь к нам...
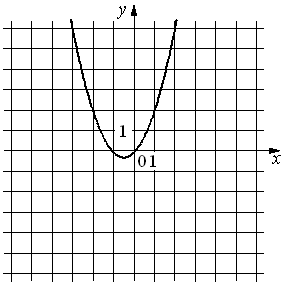 На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
| УТВЕРЖДЕНИЯ | ПРОМЕЖУТКИ |
| А) Функция возрастает на промежутке Б) Функция убывает на промежутке |
1) [-3;3] 2) [0;3] 3) [-3;-1] 4) [-3;0] |
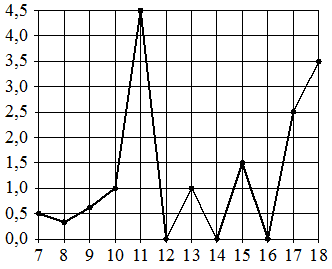 На рисунке жирными точками показано суточное количество осадков, выпадавших в Элисте с 7 по 18 декабря 2001 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки
на рисунке соединены линией. Определите по рисунку, какого числа из данного периода в Элисте выпало ровно 1,5 миллиметра осадков.
На рисунке жирными точками показано суточное количество осадков, выпадавших в Элисте с 7 по 18 декабря 2001 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки
на рисунке соединены линией. Определите по рисунку, какого числа из данного периода в Элисте выпало ровно 1,5 миллиметра осадков.
Постройте график функции 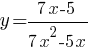 и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
На рисунке изображены графики функций вида y=kx+b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | ||
|
А) k<0, b<0 Б) k<0, b>0 В) k>0, b<0 |
1)  |
2)  |
|
3)  |
4)  |
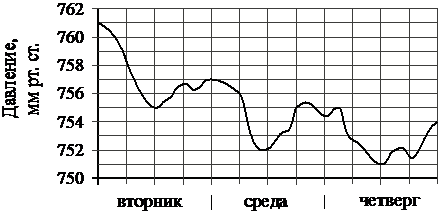 На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели и время, по вертикали – значения атмосферного давления в миллиметрах ртутного столба. Укажите значение атмосферного давления (в мм рт. ст.) в среду в 18 часов вечера. Ответ дайте в мм рт. ст.
На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели и время, по вертикали – значения атмосферного давления в миллиметрах ртутного столба. Укажите значение атмосферного давления (в мм рт. ст.) в среду в 18 часов вечера. Ответ дайте в мм рт. ст.
Комментарии: