Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) y=-x2+2x+5
Б) y=x2+2x-5
В) y=-x2-2x+5
ГРАФИКИ
1) 
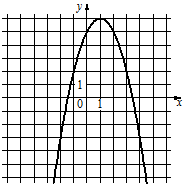2) 
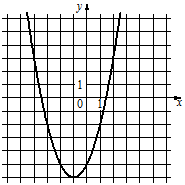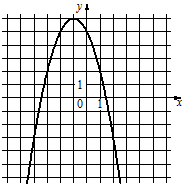
3) 
В таблице под каждой буквой укажите соответствующий номер.
Рассмотрим каждую функцию:
А) y=-x2+2x+5
Коэффициент при x2 (он же "а") равен -1, т.е. меньше нуля, следовательно, ветви параболы направлены вниз. Получается, что может подойти или график 1), или график 3).
Найдем координаты вершины параболы для нашей функции (по формуле x0=-b/(2a)):
x0=-2/(2*(-1))=-2/(-2)=1.
Посмотрим на графики, из выбранных нами графиков только у графика 1) координата x0=1, т.е. функции А) соответствует график 1).
Б) y=x2+2x-5
Коэффициент "а" у этой функции равен 1, т.е. больше нуля, следовательно, ветви параболы направлены вверх.
Только у графика 2) ветви направлены вверх, т.е. он и соответствует данной функции.
В) y=-x2-2x+5
Коэффициент "а" у этой функции равен -1, т.е. меньше нуля, следовательно, ветви параболы направлены вниз.
Методом исключения, данной функции соответствует график 3).
Ответ:
| ФУНКЦИИ | А) | Б) | В) |
| ГРАФИКИ | 1) | 2) | 3) |
Поделитесь решением
Присоединяйтесь к нам...
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
А)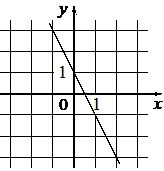 
Б) 
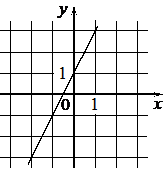В)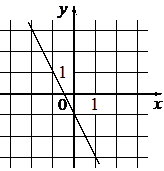 
ФОРМУЛЫ
1) y=-3x+3
2) y=3x
3) y=3x-3
В таблице под каждой буквой укажите соответствующий номер.
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
Б) 
В) 
Постройте график функции y=|x2-x-2|. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
| УТВЕРЖДЕНИЯ | ПРОМЕЖУТКИ |
| А) Функция возрастает на промежутке Б) Функция убывает на промежутке |
1) [-3;3] 2) [0;3] 3) [-3;-1] 4) [-3;0] |
Постройте график функции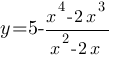 
и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: