На рисунках изображены графики функций вида y=ax2+bx+c. Установите соответствие между знаками коэффициентов a и c и графиками функций.
КОЭФФИЦИЕНТЫ
А) a>0, c<0
Б) a>0, c>0
В) a<0, c>0
ГРАФИКИ
1) 
2) 
3) 
В таблице под каждой буквой укажите соответствующий номер.
Знак коэффициента "а" определить очень легко. Если ветви графика направлены вверх, то а>0, если вниз, то a<0.
Знак коэффициента "с" можно определить следующим образом:
Приравняем "x" к нулю, тогда:
y=ax2+bx+c=a*02+b*0+c=c
Т.е. точка принадлежащая графику имеет координаты (0;c).
Это означает, что точка пересечения графика и оси Y показывает знак "с", а именно, если пересечение находится над осью X, то c>0, а если под осью X, то c<0.
Теперь надо только сопоставить.
Ответ:
| ФУНКЦИИ | А) | Б) | В) |
| КОЭФФИЦИЕНТЫ | 1) | 2) | 3) |
Поделитесь решением
Присоединяйтесь к нам...
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
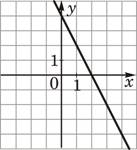
А) y=-2x+4
Б) y=2x-4
В) y=2x+4
ГРАФИКИ
1) 
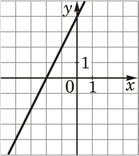2) 
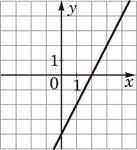3) 
В таблице под каждой буквой укажите соответствующий номер.
Постройте график функции
Определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
Постройте график функции y=|x|x-|x|-3x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
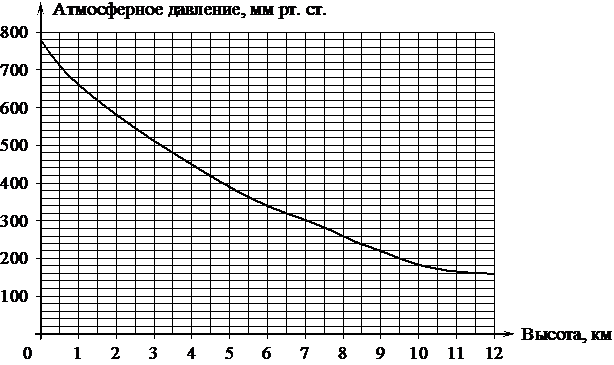На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). Найдите, чему равно атмосферное давление на высоте 7,5 км. Ответ дайте в миллиметрах ртутного столба.
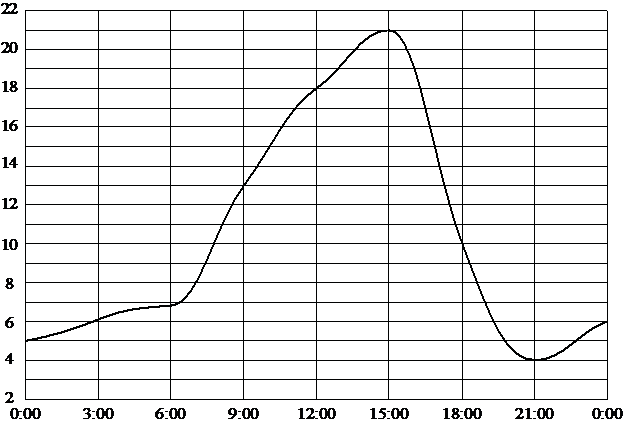На рисунке показано, как изменялась температура на протяжении одних суток. По горизонтали указано время суток, по вертикали – значение температуры в градусах Цельсия. Сколько часов во второй половине суток температура превышала 10°C?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: