
Постройте график функции y=|x|x-|x|-3x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Данная функция содержит
модуль, следовательно ее нужно разложить на две функции:
 x*x-x-3x, при x≥0
x*x-x-3x, при x≥0
(-x)x-(-x)-3x, при x<0
 x2-4x, при x≥0
x2-4x, при x≥0
-x2-2x, при x<0
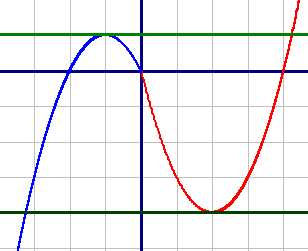 Обе подфункции - параболы. Построим их по точкам:
Обе подфункции - параболы. Построим их по точкам:
y1=x2-4x (красный график)
| X | 0 | 1 | 2 | 3 | 4 |
| Y | 0 | -3 | -4 | -3 | 0 |
| X | 0 | -1 | -2 | -3 |
| Y | 0 | 1 | 0 | -3 |
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции 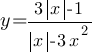 и определите, при каких значениях k прямая y=kx не имеет с графиком ни одной общей точки.
и определите, при каких значениях k прямая y=kx не имеет с графиком ни одной общей точки.
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ
А)  Б)
Б)  В)
В) 
КОЭФФИЦИЕНТЫ
1) k<0, b>0
2) k<0, b<0
3) k>0, b>0
В таблице под каждой буквой укажите соответствующий номер.
Постройте график функции 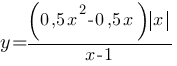 и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
Постройте график функции y=x2-6|x|-2x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
Постройте график функции 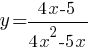 .
.
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Комментарии: