Постройте график функции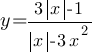 
и определите, при каких значениях k прямая y=kx не имеет с графиком ни одной общей точки.
В данной функции присутствуем
модуль, следовательно функцию надо разложить на две подфункции, в зависимости от значения
модуля:
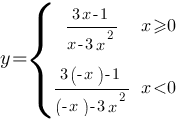
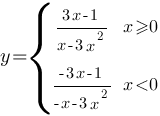
Теперь надо построить график каждой подфункции в его границах и объединить их.
1) 
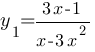, при х≥0.
Напишем Область Допустимых Значений (ОДЗ).
Так как знаменатель не может равняться нулю, то x-3x2≠0 Следовательно:
x(1-3x)≠0
x1≠0
x2≠1/3
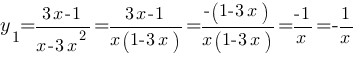
График представляет из себя гиперболу, отметим несколько точек:
| X | 0,5 | 1 | 2 |
| Y | -2 | -1 | -0,5 |
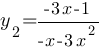, при х<0.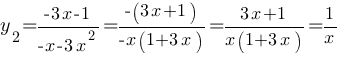
| X | -0,5 | -1 | -2 |
| Y | -2 | -1 | -0,5 |
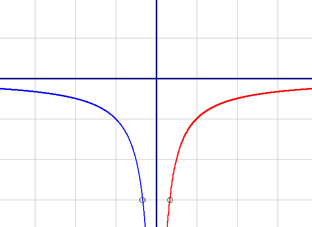График первой подфункции начерчен красным цветом, второй подфункции - синим.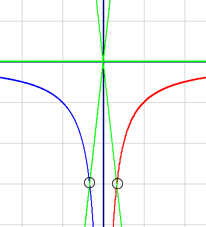
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции
x2-6x+11 при x≥2
x+1 при x<2
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
| УТВЕРЖДЕНИЯ | ПРОМЕЖУТКИ |
| А) Функция возрастает на промежутке Б) Функция убывает на промежутке |
1) [0; 2] 2) [2; 5] 3) [4; 7] 4) [1; 7] |
Постройте график функции 
и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
Постройте график функции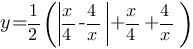 
и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Постройте график функции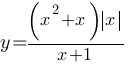
-x2+10x-21 при x≥3
-x+3 при x<3
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2020-05-18 22:04:04) Администратор: Настя, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и мы ее обязательно добавим.
(2020-05-18 11:17:02) Настя : Постройте график функции у= ((х – 1)(х^2 – 5х +6))/(х – 1) и определите, при каких значениях М прямая у= М имеет с графиком ровно одну общую точку.
(2016-05-25 22:04:50) Администратор: pU, а почему k не может быть равно 0? В условии таких ограничений нет.
(2016-05-25 13:57:45) pU: у=кх- прямая пропорциональность, где к не равен нулю почему в ответе берут к=о
(2015-10-28 21:12:14) Наталья: Огромное спасибо, за подробный разбор! Вы молодцы, лучший сайт из просмотренных! А главное наглядно и разумно! Спасибо!
(2015-05-14 22:20:21) : У вас самый лучший сайт,всё очень понятно, спасибо вам большое!
(2015-03-26 23:30:27) Анастасия: Благодарю, с вашей помощью удалось решить правильно
(2014-10-25 20:54:27) светлана: Все очень понятно, спасибо!