
Постройте график функции 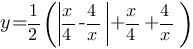 и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
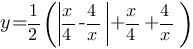
Область Допустимых Значений (ОДЗ).
x≠0 (так как делить на ноль нельзя).
Так как функция содержит
модуль, то ее надо разложить на две подфункции:
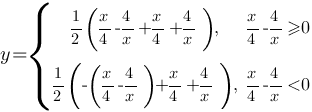
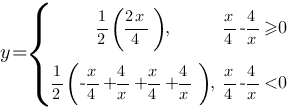
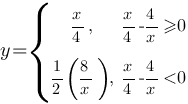
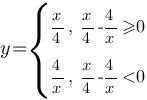
Теперь найдем для каких х 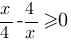 , а для каких х
, а для каких х 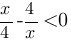
Найдем эти диапазоны:
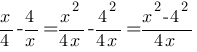
Дробь больше нуля в двух случаях:
1) Когда и числитель и знаменатель больше нуля.
2) Когда и числитель и знаменатель меньше нуля.
Эта же дробь будет меньше нуля на всех остальных диапазонах.
Рассмотрим первый вариант:
 x2-42≥0
x2-42≥0
4x>0
Чтобы решить систему неравенств нужно решить каждое неравенство по отдельности и пересечь полученные диапазоны.
 x2-42≥0
x2-42≥0
x>0
Диапазон второго неравенства (0;+∞), а диапазон для первого неравенства найдем, решив уравнение x2-42=0
 Воспользуемся формулой
разность квадратов:
Воспользуемся формулой
разность квадратов:
(x-4)(x+4)=0
x1=4
x2=-4
Коэффициент а=1, т.е. больше нуля, следовательно, ветви параболы направлены вверх. Значит диапазон для первого неравенства:
(-∞;-4]∪[4;+∞).
Пересекаем с диапазоном второго неравенства:
(-∞;-4]∪[4;+∞)∩(0;+∞)=[4;+∞)
Рассмотрим второй случай, когда и числитель и знаменатель меньше нуля.
 x2-42<0
x2-42<0
4x<0
 x2-42<0
x2-42<0
x<0
Эту систему решать не будем, а возьмем "обратные" диапазоны, т.е. для первого неравенства диапазон будет (-4;4), а для второго (-∞;0).
Пересекаем диапазоны:
(-4;4)∩(-∞;0)=(-4;0)
В итоге мы получили, что:
x/4-4/x≥0 на диапазонах (-4;0) и [4;+∞)
Следовательно:
x/4-4/x<0 на диапазонах (-∞;-4) и (0;4).
|
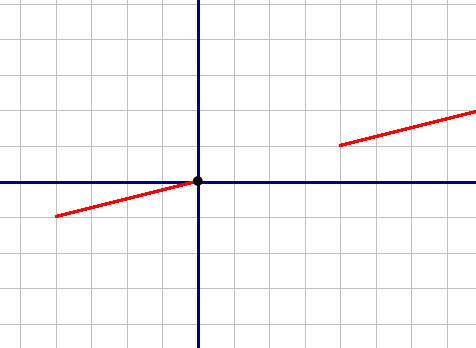
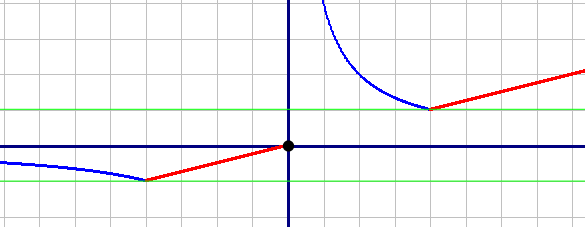
Построим график функции y1=x/4, при x∈(-4;0) и [4;+∞) - это прямая: Выкалываем точку x=0 (из ОДЗ).
| ||||||||||||
|
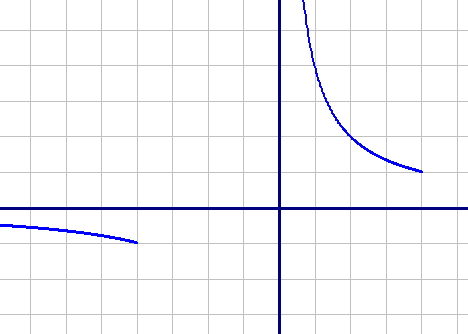
Вторая функция: y2=4/x, при x∈(-∞;-4) и (0;4) - это гипербола:
| ||||||||||||
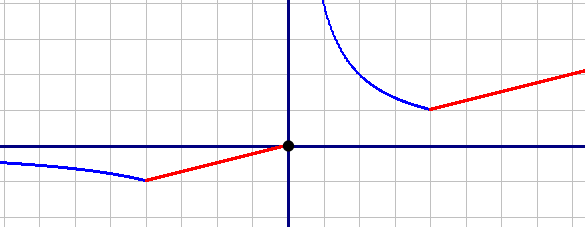
| Объединяем графики |
Поделитесь решением
Присоединяйтесь к нам...
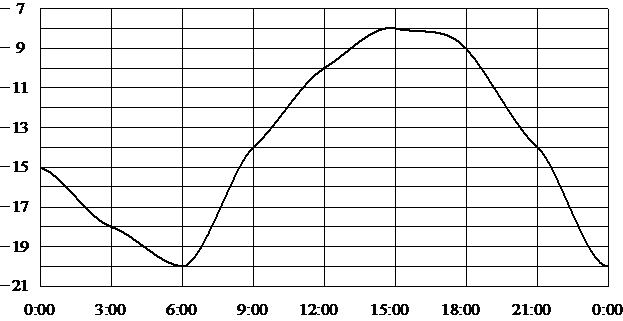 На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите разность между наибольшим и наименьшим значениями температуры во второй половине суток. Ответ дайте в градусах Цельсия.
На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите разность между наибольшим и наименьшим значениями температуры во второй половине суток. Ответ дайте в градусах Цельсия.
Установите соответствие между графиками функций и формулами, которые их задают.
| ФУНКЦИИ | ГРАФИКИ | ||
|
1) y=-6/x 2) y=-(1/2)x2 3) y=(1/2)x-2 4) y=-(1/2)x2-2 |
А)  |
Б)  |
В)  |
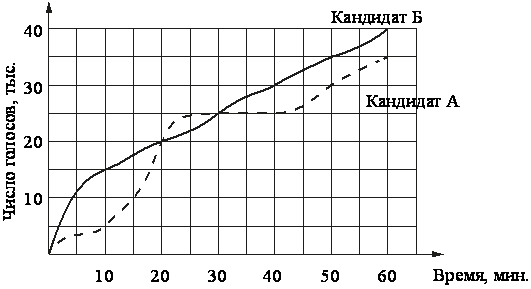 На графиках показано, как во время телевизионных дебатов между кандидатами А и Б телезрители голосовали за каждого из них. Сколько всего тысяч телезрителей проголосовало за первые 30 минут дебатов?
На графиках показано, как во время телевизионных дебатов между кандидатами А и Б телезрители голосовали за каждого из них. Сколько всего тысяч телезрителей проголосовало за первые 30 минут дебатов?
На рисунке изображены графики функций вида y=ax2+bx+c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | ||
|
1) a>0, c<0 2) a<0, c<0 3) a>0, c>0 4) a<0, c>0 |
А)  |
Б)  |
В)  |
Найдите p и постройте график функции y=x2+p, если известно, что прямая y=x имеет с графиком ровно одну общую точку.
Комментарии: