
Установите соответствие между графиками функций и формулами, которые их задают.
| ФУНКЦИИ | ГРАФИКИ | ||
|
1) y=-6/x 2) y=-(1/2)x2 3) y=(1/2)x-2 4) y=-(1/2)x2-2 |
А)  |
Б)  |
В)  |
Рассмотрим функции.
1) y=-6/x - гипербола
2) y=-(1/2)x2 - парабола
3) y=(1/2)x-2 - прямая
4) y=-(1/2)x2-2 - парабола
Рассмотрим графики.
А) - Прямая
Б) - Гипербола
В) - Парабола
Сразу можно сопоставить прямые: 3) - А) и гиперболы 1) - Б).
Теперь надо понять, какая из функций y=-(1/2)x2 или y=-(1/2)x2-2 соответствует графику В).
Проверим, подставив ноль вместо х в обе функции, судя по графику мы должны получить тоже ноль.
2) y(0)=-(1/2)*02=0
4) y(0)=-(1/2)*02-2=-2
Т.е. подходит только функция 2).
Ответ: А) - 3), Б) - 1), В) - 2)
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции 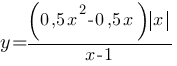 и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
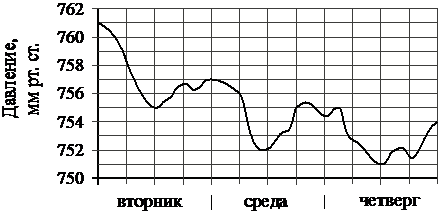 На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели и время, по вертикали – значения атмосферного давления в миллиметрах ртутного столба. Укажите значение атмосферного давления (в мм рт. ст.) в среду в 18 часов вечера. Ответ дайте в мм рт. ст.
На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели и время, по вертикали – значения атмосферного давления в миллиметрах ртутного столба. Укажите значение атмосферного давления (в мм рт. ст.) в среду в 18 часов вечера. Ответ дайте в мм рт. ст.
Постройте график функции
y=x|x|-|x|-3x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Найдите все значения k, при каждом из которых прямая y=kx имеет с графиком функции y=x2+6,25 ровно одну общую точку. Постройте этот график и все такие прямые.
На рисунке изображены графики функций вида
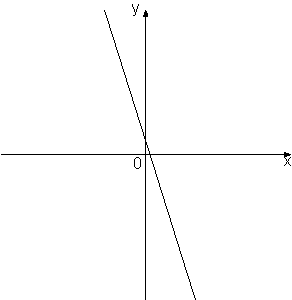
y=kx+b. Установите соответствие между знаками коэффициентов k и b и графиками.
КОЭФФИЦИЕНТЫ
А) k<0, b<0
Б) k>0, b>0
В) k<0, b>0
1)
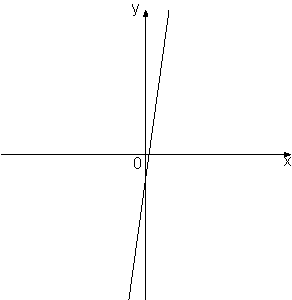
2)
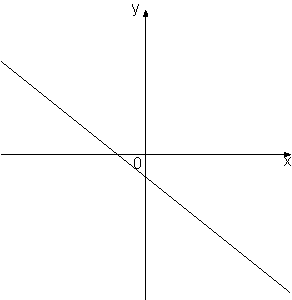
3)
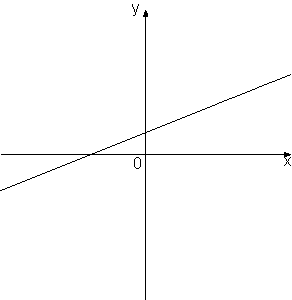
4)
Комментарии: