Постройте график функции
y=x|x|-|x|-3x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Данная функция содержит
модуль, следовательно ее нужно разложить на две функции:
x*x-x-3x, при x≥0
x*(-x)-(-x)-3x, при x<0
x2-x-3x, при x≥0
-x2+x-3x, при x<0
x2-4x, при x≥0
-x2-2x, при x<0
Рассмотрим каждую подфункцию:
1) y=x2-4x, при x≥0 (красный график)
| X | 0 | 1 | 2 | 3 |
| Y | 0 | -3 | -4 | -3 |
| X | 0 | -1 | -2 | -3 |
| Y | 0 | 1 | 0 | -3 |
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции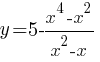 
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Постройте график функции y=x2-6|x|+8. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
А)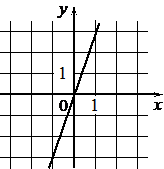 
Б) 
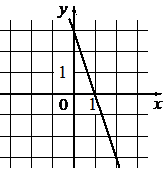В)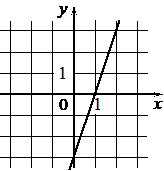 
ФОРМУЛЫ
1) y=-3x+3
2) y=3x
3) y=3x-3
В таблице под каждой буквой укажите соответствующий номер.
Постройте график функции y=x2-5|x|-x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
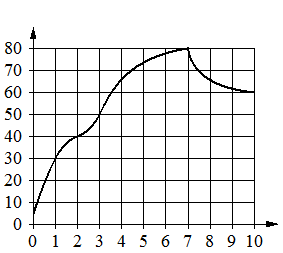На графике показано изменение температуры в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя, на вертикальной оси — температура двигателя в градусах Цельсия. Определите по графику,
через сколько минут с момента запуска двигатель нагреется до 40°C.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: