
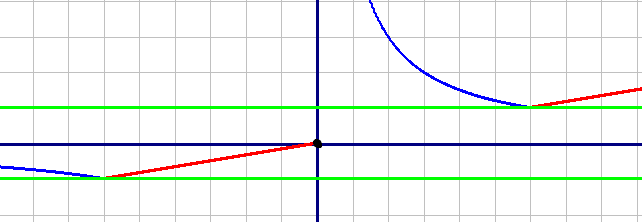
Постройте график функции
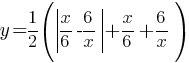
Определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Область Допустимых Значений (ОДЗ).
x≠0 (так как делить на ноль нельзя).
Так как функция содержит
модуль, то ее надо разложить на две подфункции:

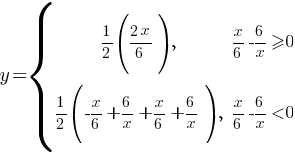
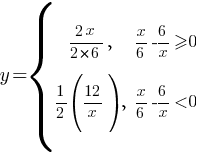
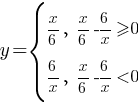
Теперь найдем для каких х 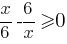 , а для каких х
, а для каких х 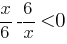
Найдем эти диапазоны.
Для начала преобразуем эту разность дробей, чтобы было легче проводить дальнейшие вычисления:
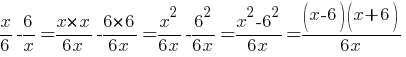
Последнее действие проводилось по формуле разность квадратов.
1) Рассмотрим первое неравенство 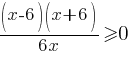 .
.
Дробь больше нуля в двух случаях:
a) Когда и числитель и знаменатель больше нуля.
b) Когда и числитель и знаменатель меньше нуля.
Рассмотрим вариант "а":
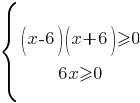
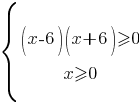
Чтобы решить систему неравенств нужно решить каждое неравенство по отдельности и пересечь полученные диапазоны.
Диапазон второго неравенства (0;+∞), а диапазон для первого неравенства найдем, решив уравнение (x-6)(x+6)=0
x1=6
x2=-6
 Коэффициент а=1, т.е. больше нуля, следовательно, ветви параболы направлены вверх. Значит диапазон для первого неравенства:
Коэффициент а=1, т.е. больше нуля, следовательно, ветви параболы направлены вверх. Значит диапазон для первого неравенства:
(-∞;-6]∪[6;+∞).
Пересекаем с диапазоном второго неравенства:
(-∞;-6]∪[6;+∞)∩(0;+∞)=[6;+∞)
Рассмотрим случай b), когда и числитель и знаменатель меньше нуля.
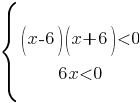
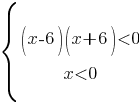
Эту систему решать не будем, а возьмем "обратные" диапазоны, т.е. для первого неравенства диапазон будет (-6;6), а для второго (-∞;0).
Пересекаем диапазоны:
(-6;6)∩(-∞;0)=(-6;0)
В итоге мы получили, что:
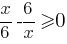 на диапазонах (-6;0) и [6;+∞)
на диапазонах (-6;0) и [6;+∞)
2) Рассмотрим второе неравенство 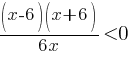 .
.
Решать это неравенство также не будем, а просто возьмем обратный диапазон от первого: (-∞;-6) и (0;6).
Запишем нашу первоначальную систему с полученными диапазонами:
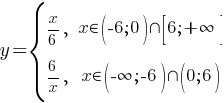
 Построим графики функций.
Построим графики функций.
Красным цветом постоим первую функцию, которая является прямой, по точкам:
| X | -6 | 0 | 6 |
| Y | -1 | 0 | 1 |
| X | -12 | -6 | 1 | 6 |
| Y | -0,5 | -1 | 6 | 1 |
Поделитесь решением
Присоединяйтесь к нам...
 На рисунке изображены графики функций y=6-x2 и y=5x. Вычислите абсциссу точки B.
На рисунке изображены графики функций y=6-x2 и y=5x. Вычислите абсциссу точки B.
Постройте график функции y=x2-4|x|-2x и определите, при каких значениях m прямая y=m имеет с графиком не менее одной, но не более трёх общих точек.
Постройте график функции 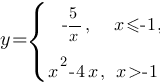 и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
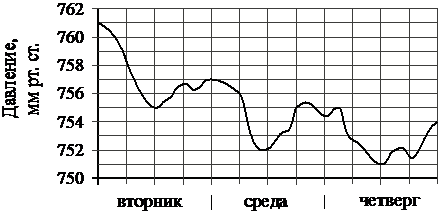 На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели и время, по вертикали – значения атмосферного давления в миллиметрах ртутного столба. Укажите значение атмосферного давления (в мм рт. ст.) в среду в 18 часов вечера. Ответ дайте в мм рт. ст.
На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели и время, по вертикали – значения атмосферного давления в миллиметрах ртутного столба. Укажите значение атмосферного давления (в мм рт. ст.) в среду в 18 часов вечера. Ответ дайте в мм рт. ст.
Постройте график функции y=x2-6|x|+2x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
Комментарии: