Постройте график функции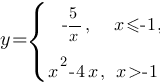 
и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
Чтобы построить график этой функции, надо построить график каждой подфункции на указанных для подфункций диапазонах.
y1=-5/x на диапазоне (-∞;-1]
y2=x2-4x на диапазоне (-1;+∞)
График первой подфункции (красный) - гипербола, строим его просто по точкам:
| X | -1 | -2 | -5 |
| Y | 5 | 2,5 | 1 |
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции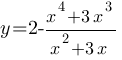 
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Известно, что графики функций y=x2+p и y=2x-2 имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
Постройте график функции
-x2-2x+2, если x≥-3,
-x-4, если x<-3,
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Постройте график функции
x2, если |x|≤1
1/x, если |x|>1
и определите, при каких значениях c прямая y=c будет иметь с графиком единственную общую точку.
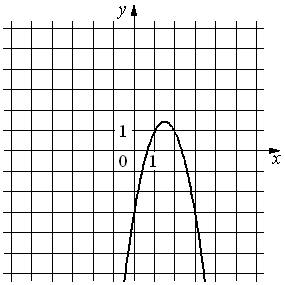На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
| УТВЕРЖДЕНИЯ | ПРОМЕЖУТКИ |
| А) Функция возрастает на промежутке Б) Функция убывает на промежутке |
1) [2;3] 2) [-2;1] 3) [-1;2] 4) [1;2] |
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: