
 Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 4. Найдите радиус окружности.
Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 4. Найдите радиус окружности.
Рассмотрим треугольник АОВ. АО=ОВ, т.к. это радиусы окружности. Следовательно,
треугольник АОВ - равнобедренный. Следовательно, /ОВА = /ОАВ (по свойству равнобедренного треугольника).
По теореме о сумме углов треугольника можем записать:
180°=/AOB+/OBA+/BAO
180°=60°+/OBA+/BAO
120°=/OBA+/BAO
А так как /OBA=/BAO, то /OBA=/BAO=120°/2=60°.
Следовательно треугольник АОВ - равносторонний (по свойству равностороннего треугольника). Следовательно, ОВ=ОА=АВ=4.
Ответ: АВ=4.
Поделитесь решением
Присоединяйтесь к нам...
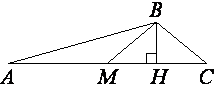 В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=216, HC=54 и ∠ACB=40°. Найдите угол AMB. Ответ дайте в градусах.
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=216, HC=54 и ∠ACB=40°. Найдите угол AMB. Ответ дайте в градусах.
 Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=5, AC=24. Найдите AO.
Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=5, AC=24. Найдите AO.
 В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 80°. Найдите величину угла OAB.
В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 80°. Найдите величину угла OAB.
Синус острого угла A треугольника ABC равен 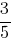 . Найдите CosA.
. Найдите CosA.
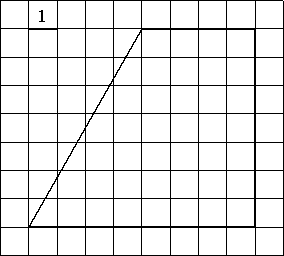 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
Комментарии: