Постройте график функции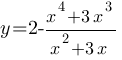 
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Отметим Область допустимых Значений (ОДЗ).
На ноль делить нельзя, следовательно:
x2+3x≠0
x(x+3)≠0
x≠0
x≠-3
Теперь упростим нашу функцию:
Получили квадратичную функцию, значит график - парабола, коэффициент а=-1 (т.е. меньше нуля), значит ветви направлены вниз.
Построим график по точкам:
| X | -2 | -1 | 0 | 1 | 2 |
| Y | -2 | 1 | 2 | 1 | -2 |
Поделитесь решением
Присоединяйтесь к нам...
Найдите все значения k, при каждом из которых прямая y=kx имеет с графиком функции y=x2+4 ровно одну общую точку. Постройте этот график и все такие прямые.
Постройте график функции
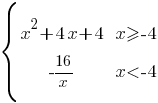
и определите, при каких значениях m прямая y=m имеет с графиком одну или две общие точки.
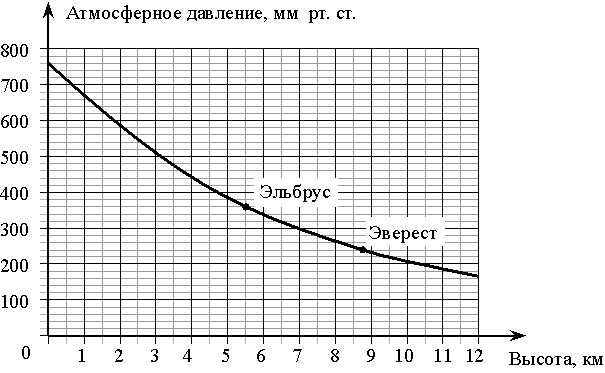На графике изображена зависимость атмосферного давления от высоты местности над уровнем моря. По горизонтали указана высота над уровнем моря в километрах, по вертикали — атмосферное давление в миллиметрах ртутного столба. На сколько миллиметров ртутного столба атмосферное давление на высоте Эвереста ниже атмосферного давления на высоте Эльбруса?
Две прямые пересекаются в точке C (см. рис.). Найдите абсциссу точки C.
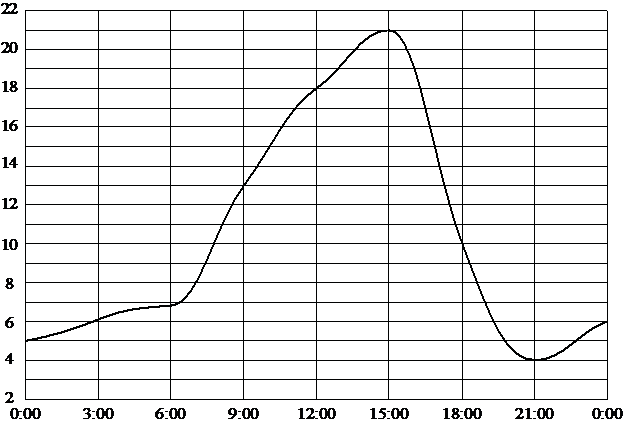На рисунке показано, как изменялась температура на протяжении одних суток. По горизонтали указано время суток, по вертикали – значение температуры в градусах Цельсия. Сколько часов во второй половине суток температура превышала 10°C?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-04-14 19:14:33) Администратор: Одна выколотая точка - это когда x=-3, y(-3)=2-(-3)2=2-9=-7, вторая - когда x=0, y(0)=2-02=2
(2015-04-14 19:02:34) : Как мы определили , что =-7. y=2.