
Постройте график функции y=|x|x+|x|-6x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Данная функция содержит
модуль, следовательно ее нужно разложить на две функции:
 x*x+x-6x, при x≥0
x*x+x-6x, при x≥0
(-x)x+(-x)-6x, при x<0
 x2-5x, при x≥0
x2-5x, при x≥0
-x2-7x, при x<0
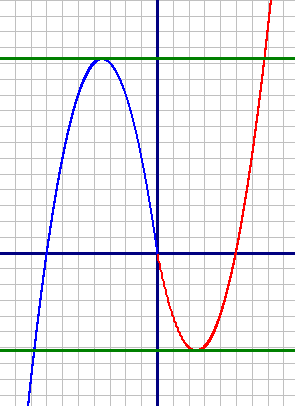 Обе подфункции - параболы. Построим их по точкам:
Обе подфункции - параболы. Построим их по точкам:
y1=x2-5x (красный график)
| X | 0 | 1 | 2 | 3 |
| Y | 0 | -4 | -6 | -6 |
| X | 0 | -1 | -2 | -3 |
| Y | 0 | 6 | 10 | 12 |
Поделитесь решением
Присоединяйтесь к нам...
Найдите значение выражения 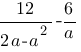 при a=-23.
при a=-23.
При каких значениях р вершины парабол у=х2+4рх-1 и у=-х2+6рх-р расположены по разные стороны от оси х?
Найдите значение выражения 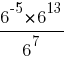
Найдите значение выражения 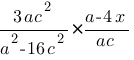 при a=2,1, c=-0,4.
при a=2,1, c=-0,4.
Решите уравнение (x2-36)2+(x2+4x-12)2=0.
Комментарии: