Решение задачи:

Рассмотрим предложенные квадратные уравнения:
В первом уравнении а=-1, т.е. меньше 0, значит ветви этой параболы смотрят вниз;
во-втором уравнении а=1, т.е. больше 0, значит ветви смотрят вверх.
Возможны два варианта:
1) Первый график пересекает ось х, а второй не пересекает, как на рисунке 1.
2) Первый график не пересекает ось х, а второй пересекает, как на рисунке 2.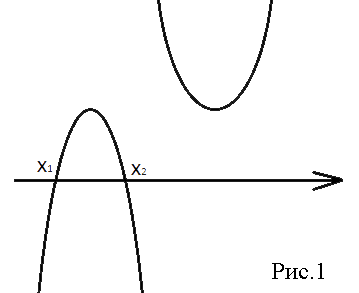
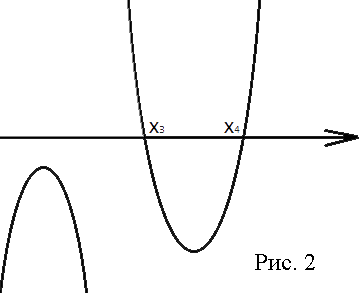
Рассмотрим каждый вариант:
1) Чтобы график первой функции пересекал ось х, уравнение должно иметь корни, следовательно, дискриминант этого уравнения должен быть больше нуля. А дискриминант второго, соответственно, меньше нуля.
D₁=(-6m)²-4(-1)m=36m²+4m>0
D₂=(-4m)²-4*1(-2)=16m²+8<0
Обратим внимание на второе неравенство:
16m²+8<0
16m²<-8
m²<-1/2
Квадрат любого числа не может быть меньше отрицательного числа, следовательно, этот вариант не подходит. Рассмотрим второй вариант:
2) Чтобы график первой функции не пересекал ось х, уравнение не должно иметь корней, следовательно, дискриминант этого уравнения должен быть меньше нуля. А дискриминант второго, соответственно, больше нуля.
D₁=(-6m)²-4(-1)m=36m²+4m<0
D₂=(-4m)²-4*1(-2)=16m²+8>0
Решим эту систему неравенств:
36m²+4m<0
16m²+8>0
9m²+m<0
2m²+1>0
Чтобы решить первое неравенство найдем корни уравнения 9m²+m=0
m(9m+1)=0
m₁=0
m₂=-1/9
Первое неравенство верно на диапазоне (-1/9;0)
Решим второе неравенство:
2m²+1>0
m²>-1/2
Второе неравенство верно при любых m, т.к. квадрат любого числа всегда больше любого отрицательного числа.
Следовательно, решение данного неравенства диапазон (-∞;+∞)
Пересекаем решения обоих неравенств, получаем решение системы неравенств:
m⊂(-1/9; 0)
Ответ: m⊂(-1/9; 0)