
Найдите сумму всех положительных членов арифметической прогрессии 11,2; 10,8; …
Для начала найдем
разность арифметической прогрессии:
d=a2-a1=10,8-11,2=-0,4
Теперь найдем сколько членов этой прогрессии являются положительными:
an>0
an=a1+d(n-1)>0
11,2-0,4(n-1)>0
11,2-0,4n+0,4>0
11,6-0,4n>0
11,6>0,4n |:0,4
29>n
n - это натуральное целое число, следовательно nmax=28
Остается только найти сумму первых 28-и членов этой прогрессии, для этого воспользуемся
формулой:
S28=(2a1+(n-1)d)*n/2=(2*11,2+(28-1)(-0,4))28/2=(22,4+27*(-0,4))14=(22,4-10,8)14=11,6*14=162,4
Ответ: 162,4
Поделитесь решением
Присоединяйтесь к нам...
Найдите значение выражения 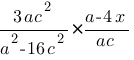 при a=2,1, c=-0,4.
при a=2,1, c=-0,4.
Мощность постоянного тока (в ваттах) вычисляется по формуле P=I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 283,5 Вт, а сила тока равна 4,5 А.
Найдите значение выражения 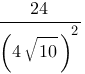
Какое из данных ниже чисел является значением выражения 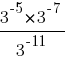 ?
?
1) -3
2) 3
3) 1/3
4) -1/3
Представьте выражение (m-9)-8*m13 в виде степени с основанием m.
1) m85
2) m-4
3) m59
4) m-30
Комментарии:
(2017-06-05 21:13:32) Администратор: Владислав, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправте заявку на добавление задачи, и мы ее обязательно добавим.
(2017-06-05 15:13:12) владислав: 9/(x-3)-3x/(x-3)^2∶3x/(x^2-9)-(2x-3)/(x-3);