Постройте график функции
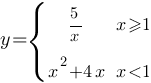и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
Чтобы построить график этой функции, надо построить график каждой подфункции на указанных для подфункций диапазонах.
y1=5/x на диапазоне [1;+∞)
y2=x2+4x на диапазоне (-∞;1)
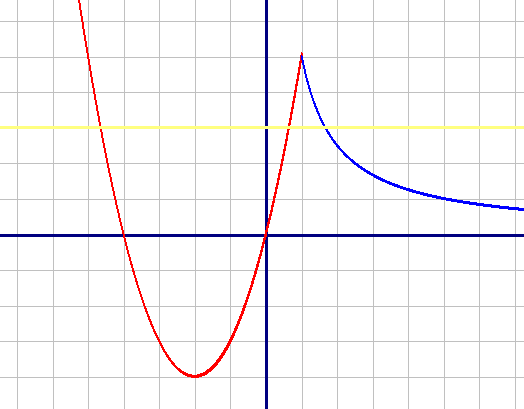График первой подфункции (синий) - гипербола, строим его просто по точкам:
| X | 1 | 2 | 5 |
| Y | 5 | 2,5 | 1 |
Поделитесь решением
Присоединяйтесь к нам...
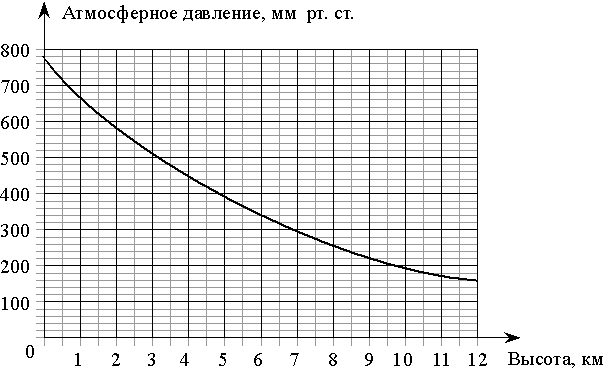На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 580 миллиметров ртутного столба?
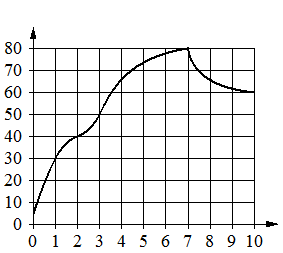На графике показано изменение температуры в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя, на вертикальной оси — температура двигателя в градусах Цельсия. Определите по графику,
через сколько минут с момента запуска двигатель нагреется до 40°C.
Постройте график функции
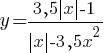
Определите, при каких значениях k прямая y=kx не имеет с графиком общих точек.
Постройте график функции y=4|x+6|-x2-11x-30 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
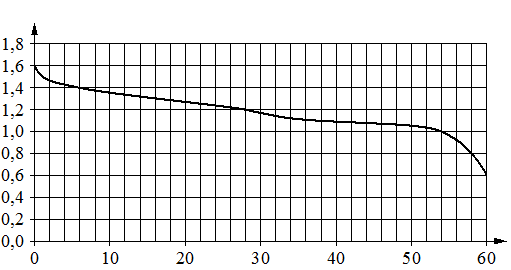При работе фонарика батарейка постепенно разряжается и напряжение
в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, за сколько часов работы фонарика напряжение упадёт с 1,4 В до 0,8 В.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: