Постройте график функции
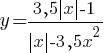
Определите, при каких значениях k прямая y=kx не имеет с графиком общих точек.
В данной функции присутствуем
модуль, следовательно функцию надо разложить на две подфункции, в зависимости от значения
модуля:
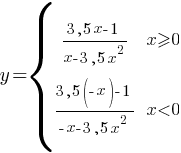
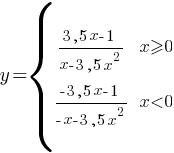
Теперь надо построить график каждой подфункции в его границах и объединить их.
1) 
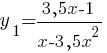, при х≥0.
Напишем Область Допустимых Значений (ОДЗ).
Так как знаменатель не может равняться нулю, то x-3,5x2≠0
Вынесем "х" за скобку:
x(1-3,5x)≠0
Произведение равно нулю, когда один из множителей равен нулю, поэтому рассмотрим два случая:
1) x1≠0
2) 1-3,5x≠0
3,5x≠1
x≠1/3,5=2/7
Теперь можно упростить функцию:
График представляет из себя гиперболу, отметим несколько точек:
| X | 0,5 | 1 | 2 |
| Y | -2 | -1 | -0,5 |
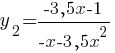, при х<0.
| X | -0,5 | -1 | -2 |
| Y | -2 | -1 | -0,5 |
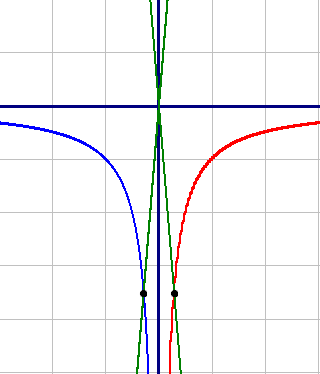График первой подфункции начерчен красным цветом, второй подфункции - синим.Поделитесь решением
Присоединяйтесь к нам...
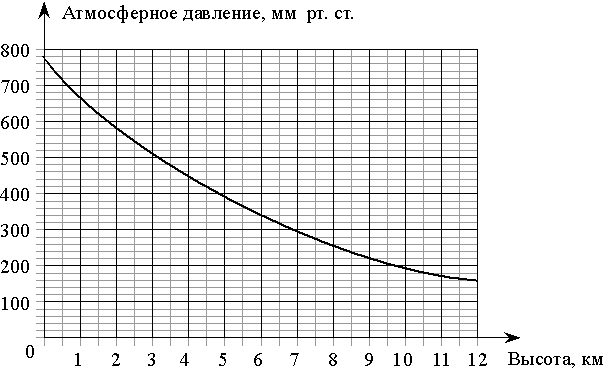На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 580 миллиметров ртутного столба?
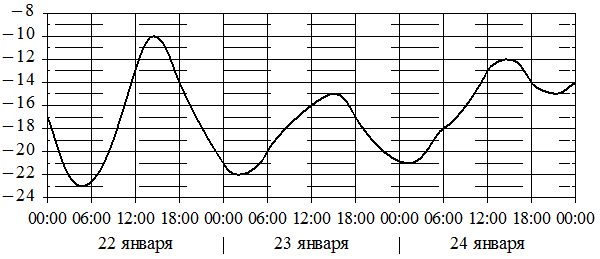На графике показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по графику наибольшую температуру воздуха 24 января. Ответ дайте в градусах Цельсия.
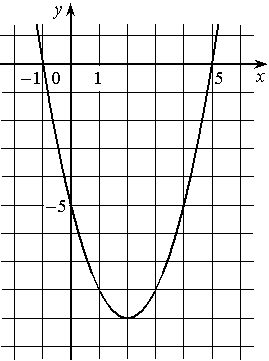На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции являются верными? Запишите их номера.
1) f(-1)=f(5)
2) Функция убывает на промежутке [2; +∞)
3) f(x)>0 при x<-1 и при x>5
Постройте график функции
-x2, если |x|≤1
-1/x, если |x|>1
и определите, при каких значениях c прямая y=c будет иметь с графиком единственную общую точку.
Постройте график функции y=|x|(x+1)-6x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: